Prolongement unique

[adamNIDO]

Bonjour,


Merci d'avance

[Doraki]

Pour ton choix de alpha il faut donc :
- que alpha ne soit pas dans l'image de f (sinon g n'est pas injective)
- que R = image de f u {alpha} (sinon g n'est pas surjective)

Donc, question à se poser immédiatement :

Quelle est l'image de f ?

[adamNIDO]

Bonjour,

si j'ai bien compris tu veux dire que :

g est un prolongement unique bijective ssi


svp j'ai pas compris pourquoi si dans Im f implique que f est non injective


Merci d'avance

[Doraki]

L'image de f ce n'est pas f(R) mais f(R privé de {1}) (enfin bon là c'est pas un abus de notation qui me paraît bien grave)

Pour l'injectivité, il faut que f elle même soit injective, sinon tu n'as bien sur aucune chance d'avoir g injective.

Si alpha = f(x) pour x<>1 (donc si alpha est dans l'image de f), alors g n'est pas injective :
x et 1 sont différents, mais g(1) = alpha = f(x) = g(x), donc g n'est pas injective.

[adamNIDO]

@ Doraki Oui j'ai compris Merci infiniment

[capitaine nuggets]

Salut !

De manière très grossière, ta fonction est une "espèce" de fonction inverse (i.e. ).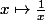
Or le seul moyen de prolonger bijectivement la fonction inverse sur consiste à associer à la valeur (seule valeur qui n'est pas dans l'image).

Ici c'est pareil, montre qu'à 1, il faudra associer 2, pour prolonger f en g.

[adamNIDO]

Bonsoir,

@capitaine nuggets Merci beaucoup