Je prends la première pièce jointe comme étant ton corrigé et ta seconde pièce jointe comme étant ton énoncé.
Déjà, il y a une sens évident : Si
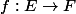
est bijective alors pour toute partie
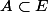
,
 = F \etminus f(A))
. Cela provient du fait que si
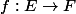
est bijective alors en particulier
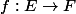
est surjective et que
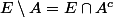
, où
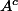
désigne le complémentaire de

dans

. Ensuite, il faut connaître les règles de calculs avec les images réciproques.
Sinon, à priori je dirais qu'on a juste
=f(E))
.

et

ont même image par

, donc si on retire

ça ne change rien, son image (qui est la même que celle de

) est toujours dans
)
. Mais je ne vois pas pourquoi
=F)
. Il faudrait pour ça que

sur surjective. Ainsi, on aurait
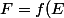= f(E\setminus A))
.

