Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JaiUneQuestion
- Membre Naturel
- Messages: 21
- Enregistré le: 17 Mar 2016, 17:18
-
 par JaiUneQuestion » 16 Mai 2016, 15:33
par JaiUneQuestion » 16 Mai 2016, 15:33
Bonjour,
Qu'est-ce qui est faux dans mon raisonnement ?
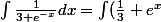 dx = \int \frac{1}{3}dx + \int e^x dx = \frac{x}{3} + e^x + c)
Merci
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 16 Mai 2016, 15:59
par Pisigma » 16 Mai 2016, 15:59
Bonjour,
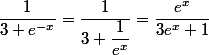
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 16 Mai 2016, 16:08
par Pisigma » 16 Mai 2016, 16:08
De rien

-
JaiUneQuestion
- Membre Naturel
- Messages: 21
- Enregistré le: 17 Mar 2016, 17:18
-
 par JaiUneQuestion » 16 Mai 2016, 16:30
par JaiUneQuestion » 16 Mai 2016, 16:30
J'essais de la résoudre, mais je ne trouve toujours pas la même chose que le corrigé.
Je pose :
u = e^x du = e^x . dx
dx = 1/u . du
} du = \frac{1}{3}\int \frac{du}{u+\frac{1}{3}})
On a une intégrale de la forme u' / u , çar (u+1/3)' = du. Donc :
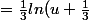 = \frac{1}{3} ln(e^x+\frac{1}{3}))
Or le corrigé dit ça :

Je ne comprends pas la présence du 3 dans leur ln.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 16 Mai 2016, 16:45
par Pseuda » 16 Mai 2016, 16:45
Bonsoir,
C'est à cause de la constante. Le résultat est le même mais pas la constante : ln (3 e^x +1) = ln 3 + ln (e^x +1/3), ce me semble.
 par MurphyCooper » 16 Mai 2016, 17:15
par MurphyCooper » 16 Mai 2016, 17:15
Et du coup en fait dans l'énoncé ils rajoutent juste une constante mais ça revient au même puisque les intégrales ne prennent pas en compte les constantes des primitives.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 16 Mai 2016, 17:18
par Pisigma » 16 Mai 2016, 17:18

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Mai 2016, 17:38
par zygomatique » 16 Mai 2016, 17:38
JaiUneQuestion a écrit:Bonjour,
Qu'est-ce qui est faux dans mon raisonnement ?
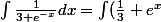 dx = \int \frac{1}{3}dx + \int e^x dx = \frac{x}{3} + e^x + c)
Merci
salut
peut-être que


et un changement de variable est inutile ... quand on connaît ses formules de dérivations ...
modulo la transformation d'écriture
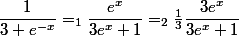
on reconnaît la formule de terminale

(et de première ku')
(1) : on multiplie numérateur et dénominateur par exp(x)
(2) : on multiplie par 1 (ce qui ne change rien) mais qu'on écrit convenablement (en l'occurrence ici
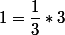
)
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités

