Bonjour, puis-je avoir une idée sur l'exercice suivant svp... Merci.
Q/ Résoudre dans C l'équation Z^6 + Z^4 + Z^2 + 1 = 0 avec tous les détails possibles.
Nombres complexes.
5 messages
- Page 1 sur 1
Re: Nombres complexes.
Salut,
"avec tout les détail", non, ça va pas être possible : c'est contraire à la charte vu que ça t'avancerais à rien de "gober tout cru" une solution trouvée par un autre.
Par contre des petites indictions, ça c'est jouable :
- Si q est un complexe différent de 1, alors 1+q+q²+...+q^n= ???
- Les racine n-ièmes de l'unité dans C (i.e. les solutions de z^n=1) sont ...
"avec tout les détail", non, ça va pas être possible : c'est contraire à la charte vu que ça t'avancerais à rien de "gober tout cru" une solution trouvée par un autre.
Par contre des petites indictions, ça c'est jouable :
- Si q est un complexe différent de 1, alors 1+q+q²+...+q^n= ???
- Les racine n-ièmes de l'unité dans C (i.e. les solutions de z^n=1) sont ...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Nombres complexes.
salut
comme au collège :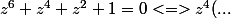 + z^2 + 1 = 0 <=> ....)
ensuite ne pas oublier que :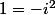
et un peu d'expérience conduit à savoir que^2 = ...)
comme au collège :
ensuite ne pas oublier que :
et un peu d'expérience conduit à savoir que
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Nombres complexes.
Salut !
Une autre méthode : résoudre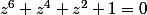 revient à résoudre, en posant
revient à résoudre, en posant 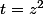 , l'équation
, l'équation 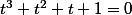 qui, elle-même, équivaut à
qui, elle-même, équivaut à (t^2+1)=0) .
.

Une autre méthode : résoudre
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Nombres complexes.
capitaine nuggets a écrit:Salut !
Une autre méthode : résoudrerevient à résoudre, en posant
, l'équation
qui, elle-même, équivaut à
.
c'est ma méthode ... tout simplement

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
