Topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 03 Mai 2016, 19:01
par kurenay » 03 Mai 2016, 19:01
Bonsoir,
On considère la partie suivante de
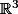
:
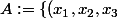\in \R^3 : 1<x^2_1+x^2_2+x^2_3 < 4 \right\})
1)Démontrer que A est ouverte dans
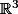
.
2) Construire un point d'adhérence de A qui n'appartient pas à A.
2) (2,0,0) appartient à R³ et 2²+0²+0²=4 appartient à Adh(A) mais n'appartient pas à A.
Merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Mai 2016, 19:30
par zygomatique » 03 Mai 2016, 19:30
salut
A est l'intersection des ouverts E= {(x, y, z) / 1 < x² + y² + z²} et F = {(x, y, z) / x² + y² + z² < 4}
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 03 Mai 2016, 19:39
par kurenay » 03 Mai 2016, 19:39
D'accord, donc je suppose qu'il faudra montrer que E et F sont des ouverts et que l'intersection de ces deux ouverts reste un ouvert donc A ouvert.
Comment je prouve que E et F sont des ouverts ?
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 03 Mai 2016, 19:55
par lionel52 » 03 Mai 2016, 19:55
C'est quoi les complémentaires de E et F?
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 03 Mai 2016, 20:23
par kurenay » 03 Mai 2016, 20:23
compl(F) = {(x, y, z) / 4

x² + y² + z²}
compl(E) = {(x, y, z) / x² + y² + z²

1}
Ils font donc montrer que compl(E) et compl(F) sont fermé ?
Modifié en dernier par
kurenay le 04 Mai 2016, 17:42, modifié 1 fois.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Mai 2016, 14:43
par zygomatique » 04 Mai 2016, 14:43
on ne peut pas faire de topologie si on n'a pas un minimum de (définition de) base ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 04 Mai 2016, 17:40
par kurenay » 04 Mai 2016, 17:40
Je pense avoir trouvé:
F = {(x, y, z) / x² + y² + z² < 4} <=>
 / \sqrt{(x-0)^2 + (y-0)^2 + (z-0)^2}< 2 \right\})
Donc
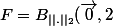)
. Donc F est ouvert.
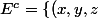 / x^2+y^2+z^2 \leq 1 \right\})
<=>
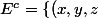 / \sqrt{(x-0)^2 + (y-0)^2 + (z-0)^2} \leq 1 \right\})
Donc
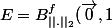)
. Donc
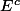
est fermé => E est ouvert
Donc A est ouverte dans R³

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Mai 2016, 19:36
par zygomatique » 04 Mai 2016, 19:36
c'est bon ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 04 Mai 2016, 20:00
par kurenay » 04 Mai 2016, 20:00
Merci pour votre aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités