Exos classiques L1-L2-L3-MPSI-MP-ECS

[M.Floquet]

Bonjour, voilà, j'ouvre un petit topic afin de proposer des grands classiques (je numéroterai les exos et essaierai de les corriger dans les jours à venir si personne a la solution, mais il manque une commande spoiler).

On commence par trois théorèmes classiques :

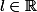
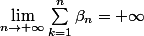
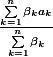
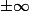
(1) : Soient une suite (réelle ou complexe) telle que converge vers et une suite de réels strictement positifs telle que . Montrer que la suite définie par : converge vers . Que dire de la réciproque ? Traiter le cas où la suite diverge vers et étudier la réciproque.

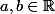
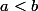
(2) : Soit continue sur cet intervalle (évidemment tel que ). Montrer que si et ne sont pas de même signe, alors il existe un réel tel que : .

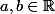
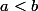
(3) : Soit tel que et continue sur cet intervalle. Montrer que admet un point fixe. Le résultat est-il encore valide si ?



Tout le monde peut évidemment contribuer à la propositions d'exercices !
Bonne chance !

[Ben314]

Salut,
Moi, je vais contribuer à... la modification de l'énoncé du troisième "exercice" (c'est un théorème archi. classique)
Le théorème c'est :
Si f:[a,b]->[a,b] (et pas [a,b]->R) est continue alors elle admet au moins un point fixe.

[M.Floquet]

Haha je vois que ce topic a du mal à décoller

[Pythales]

Pour le I, la démonstration ressemble beaucoup à celle de la moyenne de Cesaro.

[M.Floquet]

Effectivement, à quelques détails prés

[biss]

Je vais tenter 3l

[biss]

3)
f : [a,b] --> [a,b]
x [a,b]
posons g(x)=x-f(x)
comme f : [a,b]-->[a,b] on a

alors
En prenant x=a on a et comme alors
En prenant x=b on a et comme alors
donc d'après le théorème des valeurs intermédaire on a
x [a,b] tel que g(x)=0 alors
Ce qui est démontré
Non ce n est valide.

[M.Floquet]

C'est la bonne méthode pour le (3) ! Mais "pas valide" faudrait quand même expliciter un peu haha