Exercice nombres complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
SimonY
- Membre Naturel
- Messages: 35
- Enregistré le: 16 Sep 2015, 15:29
-
 par SimonY » 24 Avr 2016, 20:29
par SimonY » 24 Avr 2016, 20:29
Montrer que

si et seulement si

ou

Je sèche.. si quelqu'un pourrait me donner des pistes ce serait sympa

Merci d'avance, bonne journée.
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 25 Avr 2016, 07:41
par Manny06 » 25 Avr 2016, 07:41
calcule (a-b)(abarre-bbarre)-(1-abarre b)(1-abbarre) et constate que c'est égal à (1-aabarre)(1-bbarre)
soit |a-b|²-|1-abarreb|²=(1-|a|²)(1-|b|²)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 25 Avr 2016, 14:08
par Carpate » 25 Avr 2016, 14:08
Pour introduire en douceur le calcul de Manny06 :

est équivalent à

Or :
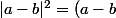(\bar{a-b})=(a-b)(\bar{a}-\bar{b}))
et :
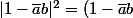(1-a\bar{b}))
Ensuite on développe :
(\bar{a}-\bar{b}) -(1-\bar{a}b)(1-a\bar{b})=0)
pour obtenir :

 -(1-b\bar{b}) = 0)
(1-b\bar{b})=0)
(1-|b|^2)=0)
etc
Modifié en dernier par
Carpate le 27 Avr 2016, 09:36, modifié 1 fois.
-
SimonY
- Membre Naturel
- Messages: 35
- Enregistré le: 16 Sep 2015, 15:29
-
 par SimonY » 26 Avr 2016, 20:28
par SimonY » 26 Avr 2016, 20:28
merci !!
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 27 Avr 2016, 09:28
par Manny06 » 27 Avr 2016, 09:28
à la 2° ligne c'est |a-b|²
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 27 Avr 2016, 09:37
par Carpate » 27 Avr 2016, 09:37
Oui, j'ai corrigé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités