Encore une Equation Differentielle

par **mari5029** » 23 Avr 2016, 17:50

Bonsoir
quelqu'un peut-il m'aider pour cette équation différentielle ? :cry:

(3y-x) - (3x+y)y' =0

Merci :cry:

par **Ben314** » 24 Avr 2016, 11:58

Salut,
Je sais pas trop si on arrive facilement à donner les solutions sous la forme

mais on arrive relativement facilement à paramétrer les solutions sous la forme

:
Avec ce point de vue, le

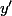
de l'équation de départ devient

=pente de la tangente en

donc l'équation devient

et, vu que la vitesse de parcours des courbes est arbitraire, on peut la prendre telle que

et on doit alors avoir

.
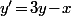
Ce qui signifie qu'on doit avoir

et donc que

avec

.
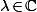
C'est à dire une Spirale logarithmique et je pense pas qu'on ait de représentations simple de la forme