Exo fonctions
16 messages
- Page 1 sur 1
Exo fonctions
bonjours a tous
F est la fonction definie sur ]1;+l'infini[ par f(x)= sqrt[x^3/(x-1)]
1) a) determiner la fonction derivée de f .
b)Etudier les variation de f
2) etudier les limites de f en 1 et en +l'infini
3) C est la courbe representant f dans un repere orthonormal
a)Démontrer que la drote D d'équation y=x+1/2 est asymtote a la courbe C en + l'infini
b) Situer la courbe C par rapport a la droite D .
1) a) je trouve f'(x)= (2x^3^-3x^2)/[2sqrt(x^3/(x-1))]
je suis bloqué sur le reste si quelqu'un pouvait m'aider merci
F est la fonction definie sur ]1;+l'infini[ par f(x)= sqrt[x^3/(x-1)]
1) a) determiner la fonction derivée de f .
b)Etudier les variation de f
2) etudier les limites de f en 1 et en +l'infini
3) C est la courbe representant f dans un repere orthonormal
a)Démontrer que la drote D d'équation y=x+1/2 est asymtote a la courbe C en + l'infini
b) Situer la courbe C par rapport a la droite D .
1) a) je trouve f'(x)= (2x^3^-3x^2)/[2sqrt(x^3/(x-1))]
je suis bloqué sur le reste si quelqu'un pouvait m'aider merci
merci je ne savais qu'il suffisait de preciser que les autres termes étaient >o pour pouvoir étudier le signe de f'(x)
b) alors j'ai trouver que f était decroisant de 1 a 3/2 et croissante de 3/2 a +l'infinit
2) la j'ai trouver limite lorsque x tend vers 1+ est egale à + l'infini
limite lorsque x tend vers 1- est egale à - l'infini
limite lorsque x tend vers +l'infini est egale à + l'infini
3) a) j'ai essayer de prouver que y=x+1/2 était asymptote a la courbe:
donc si y asymptote a la courbe alors :
lim lorsque x tend vers +l'infinit (et - l'infinit) [ f(x) - (x+1/2)]= 0
mais je narrive pas faire cette la diffenrence c'est la racine qui me gene meme en multipluant par la partie conjugué a moins que j'ai fait un erreur si quelqu'un pouvait me mette le detail du calcul ?
b) alors j'ai trouver que f était decroisant de 1 a 3/2 et croissante de 3/2 a +l'infinit
2) la j'ai trouver limite lorsque x tend vers 1+ est egale à + l'infini
limite lorsque x tend vers 1- est egale à - l'infini
limite lorsque x tend vers +l'infini est egale à + l'infini
3) a) j'ai essayer de prouver que y=x+1/2 était asymptote a la courbe:
donc si y asymptote a la courbe alors :
lim lorsque x tend vers +l'infinit (et - l'infinit) [ f(x) - (x+1/2)]= 0
mais je narrive pas faire cette la diffenrence c'est la racine qui me gene meme en multipluant par la partie conjugué a moins que j'ai fait un erreur si quelqu'un pouvait me mette le detail du calcul ?
re, pour les variations ok
pour la limite en 1 on a pas besoin de celle en 1- car on te donne l'intervalle d'etude au depart qui est ]1,+inf[ sinon c'est bon c'est bien +inf qd x->1 et +inf qd x->+inf
je regarde la 3)
2) la j'ai trouver limite lorsque x tend vers 1+ est egale à + l'infini
limite lorsque x tend vers 1- est egale à - l'infini
limite lorsque x tend vers +l'infini est egale à + l'infini
pour la limite en 1 on a pas besoin de celle en 1- car on te donne l'intervalle d'etude au depart qui est ]1,+inf[ sinon c'est bon c'est bien +inf qd x->1 et +inf qd x->+inf
je regarde la 3)
bon c'est un peu barbare comme calcul donc apres revois le à t^te reposé
)
)(\sqrt{\frac{x^3}{x-1}}+(x+\frac{1}{2}))}{\sqrt{\frac{x^3}{x-1}}+x+\frac{1}{2}})
^2}{\sqrt{\frac{x^3}{x-1}}+x+\frac{1}{2}})
donc apres avoir reduit au même denominateur et simplifié j'obtiens:
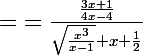
donc on factorise par x car c'est en +inf donc:
}{x(4-\frac{4}{x})}}{x(\sqrt{\frac{1}{1-\frac{1}{x}}+1+\frac{1}{2x}}))
}{(4-\frac{4}{x})}}{x(\sqrt{\frac{1}{1-\frac{1}{x}}+1+\frac{1}{2x}}))
et en passant à la limite en +inf ça fait bien 0 donc y=x+1/2 est bien asymptote oblique en +inf
j'ai passé certain details je pense que tu peux les trouver
donc apres avoir reduit au même denominateur et simplifié j'obtiens:
donc on factorise par x car c'est en +inf donc:
et en passant à la limite en +inf ça fait bien 0 donc y=x+1/2 est bien asymptote oblique en +inf
j'ai passé certain details je pense que tu peux les trouver
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 154 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
