Bonsoir tout le monde
Alors, j'ai des exercices à faire concernant la leçon des fonctions linéaires et je n'y comprends que dalle. Si vous avez un peu de temps pour m'aider à les faire et à les comprendre, je vous serais reconnaissante.
Exo 1 : f et g sont deux fonctions qui sont définies par les données suivantes :
( Ce sont deux tableaux )
x | -2 | 0 | 5 | 4 |
g(x) | 0 | 2| 3 | 4 |
x | 2 | 4 | -4 | 3 |
f(x) | 3 | 6 | -6 | 4,5 |
Sont-elles linéaires ?
Alors, pour être sincère, j'ai beau essayer trouver une réponse que je peux exprimer mathématiquement, mais en vain. J'arrive un peu à comprendre comment faire mais pas à y répondre à l'écrit. J'espère que vous voyez ce que je veux dire.
Exo 2 : Réponds par vrai ou faux :
1- Aux élections municipales, on a 1275 votes. Un élu a obtenu 60% des votes, donc 765 ont voté pour lui. Vrai ou faux ?
2- Le prix d'un produit est de 1250euros, son prix a diminué de 50euros alors le pourcentage de la réduction est de 40%. Vrai ou faux ?
3- Un produit dont le prix original est de 25euros, a augmenté de prix et est devenue à 45euros. Alors le pourcentage de l'augmentation est 160%. Vrai ou faux ?
Je ne dis pas que je suis incapable de résoudre cet exercice de la manière ordinaire, mais ce qui m'est demandé est d'y répondre en me servant de la leçon des fonctions linéaires.
J'ai besoin de réponses avant demain matin car je dois les rendre.. Mais sinon, vos réponses ne seront pas de refus après, car j'ai besoin de comprendre.
Merci d'avance,
Cordialement.
Fonctions linéaires.
11 messages
- Page 1 sur 1
Re: Fonctions linéaires.
Pour le deuxième, j'ai trouvé ceci :
1- f(1275) = 1275 * 60% = 1275*0.6 = 765. Donc vrai.
2- f(1250)=1250*40% = 1250*0.4= 500 ( je n'en suis pas sûre ).
3- f(25) = 25*160% = 25*1.6 = 40. Donc vrai.
1- f(1275) = 1275 * 60% = 1275*0.6 = 765. Donc vrai.
2- f(1250)=1250*40% = 1250*0.4= 500 ( je n'en suis pas sûre ).
3- f(25) = 25*160% = 25*1.6 = 40. Donc vrai.
Re: Fonctions linéaires.
supposons g linéaire, il existe 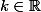
tel que
=kx_1 , \, g(x_2)=kx_2)
=kx_1 x_2 , \, x_1g(x_2)=kx_2x_1)
-x_1g(x_2)=0) (*)
(*)
réciproquement,
on teste pour les couples (x_i;g(x_i)) pour tout i, si l'on a l'égalité (*)
si oui , le tableau est un tableau de proportionnalité , il existe k tel que
g(x)=kx. Le tableau est un tableau de valeurs d'une fonction linéaire.
Notamment la deuxième fonction ,f, vérifie les égalités (*).
tel que
réciproquement,
on teste pour les couples (x_i;g(x_i)) pour tout i, si l'on a l'égalité (*)
si oui , le tableau est un tableau de proportionnalité , il existe k tel que
g(x)=kx. Le tableau est un tableau de valeurs d'une fonction linéaire.
Notamment la deuxième fonction ,f, vérifie les égalités (*).
Re: Fonctions linéaires.
Bonjour,
Je ne sais pas, c'est peut-être la question qui est mal posé, et c'est sans doute la réponse attendu à l'exercice. Mais il existe un tas de fonction non linéaire qui passent par les points (2;3), (4;6), (-4;-6) et (3;4,5).
Certes, on a un tableau de proportionnalité, mais de là à dire que f est linéaire, je trouve que c'est allez un peu vite en besogne ^^'. L'énoncé est un peu mal formulé je pense.
mathelot a écrit:supposons g linéaire, il existe
tel que(*)
réciproquement,
on teste pour les couples (x_i;g(x_i)) pour tout i, si l'on a l'égalité (*)
si oui , le tableau est un tableau de proportionnalité , il existe k tel que
g(x)=kx. Le tableau est un tableau de valeurs d'une fonction linéaire.
Notamment la deuxième fonction ,f, vérifie les égalités (*).
Je ne sais pas, c'est peut-être la question qui est mal posé, et c'est sans doute la réponse attendu à l'exercice. Mais il existe un tas de fonction non linéaire qui passent par les points (2;3), (4;6), (-4;-6) et (3;4,5).
Certes, on a un tableau de proportionnalité, mais de là à dire que f est linéaire, je trouve que c'est allez un peu vite en besogne ^^'. L'énoncé est un peu mal formulé je pense.
Re: Fonctions linéaires.
Ah oui pardon, c'est la question :
qui est mal posé, mais effectivement, il n' y a qu'un seul tableau qui peut correspondre à
celui d'une application linéaire ^^'
sakuracce a écrit:Sont-elles linéaires ?
qui est mal posé, mais effectivement, il n' y a qu'un seul tableau qui peut correspondre à
celui d'une application linéaire ^^'
Re: Fonctions linéaires.
Euh..En fait, j'ai du mal à comprendre la manière dont je peux montrer qu'une fonction est bien linéaire. Vos formules me paraissent mystérieuses, mathelot. Pourriez-vous m'expliquer un peu tout ça avec des formules plus simples ?
Merci.
Merci.
Re: Fonctions linéaires.
pour avoir une fonction linéaire, il faut que les
différents produits en croix du tableau de valeurs de f soient égaux:

 - (-4) \times 6 =0)
etc..
différents produits en croix du tableau de valeurs de f soient égaux:
etc..
Re: Fonctions linéaires.
Bonjour,
La fonction linéaire n'est pas un objet mathématique très compliqué. Tu l'utilises chaque jour au supermarché, par exemple. Comment?
Un kilo de pommes coute 3 euros.... Tu achètes 4 kilos. Combien dois-tu payer?
Tu fais (nombre de kilos)*(prix d'un kilo) = 4*3 = 12 euros
On a utilisé la fonction qui, au nombre de kilos, associe le prix total à payer. On peut noter cette fonction "f".
On a donc f(x) = 3*x
On dit qu'une telle fonction est linéaire, parce que elle ne fait que "multiplier" l'antécédent x par une valeur fixe (ici, c'est 3 qu'on appelle coefficient directeur ou bien coefficient de proportionnalité).
Le but est donc de savoir si les fonctions f et g sont linéaires, c'est à dire si elles peuvent modéliser une situation "supermarché". Prenons la fonction g:
g(0) = 2
Alors tu rentres dans un supermarché, tu achètes "0 kilos" (donc rien du tout).. et dois payer 2 euros quand même. Est-ce que c'est une situation de proportionnalité ?
Si on veut l'écrire plus mathématiquement, on doit disposer d'un unique nombre "a" fixé (qui est donc le coefficient dont je t'ai parlé) tel que g s'écrive: g(x) = a*x pour tout nombre x
Mais g(4) = 4, donc a*4 = 4 donc a = 1
Et g(5) = 3, donc a*5 = 3, donc a = 3/5
Donc ce nombre a unique n'existe pas puisqu'il est différent selon le x que tu choisis.... On est en train de multiplier chaque x par un truc différent et donc g ne peut être linéaire !
Pour f, la situation est différente. Regardons. Supposons que f(x) = m*x (avec m un nombre fixé)
f(2) = 3
donc 2*m = 3 donc m = 3/2
Mais aussi f(4) = 6
donc m*4 = 6, donc m = 6/4 = 3/2
Si tu fais avec toutes les valeurs du tableau, tu vas trouver toujours m = 3/2, donc f est bien une fonction linéaire. En effet, c'est un tableau de proportionnalité: tu achètes x kilos, tu payes 3/2*x euros. C'est logique.
Alors que pour g, ce n'est pas le cas: tu peux acheter 4 kilos et payer 4 euros, ne rien acheter et payer 2 euros... c'est pas de la proportionnalité.
En ce qui concerne ton exercice 2, c'est une bonne approche que tu as, mais tu utilises la même lettre pour désigner une fonction linéaire "f" (tu devrais/aurais du changer la notation parce que ce sont des fonctions différentes avec des coefficients différents).
La fonction linéaire n'est pas un objet mathématique très compliqué. Tu l'utilises chaque jour au supermarché, par exemple. Comment?
Un kilo de pommes coute 3 euros.... Tu achètes 4 kilos. Combien dois-tu payer?
Tu fais (nombre de kilos)*(prix d'un kilo) = 4*3 = 12 euros
On a utilisé la fonction qui, au nombre de kilos, associe le prix total à payer. On peut noter cette fonction "f".
On a donc f(x) = 3*x
On dit qu'une telle fonction est linéaire, parce que elle ne fait que "multiplier" l'antécédent x par une valeur fixe (ici, c'est 3 qu'on appelle coefficient directeur ou bien coefficient de proportionnalité).
sakuracce a écrit:
( Ce sont deux tableaux )
x | -2 | 0 | 5 | 4 |
g(x) | 0 | 2| 3 | 4 |
x | 2 | 4 | -4 | 3 |
f(x) | 3 | 6 | -6 | 4,5 |
Sont-elles linéaires ?
Le but est donc de savoir si les fonctions f et g sont linéaires, c'est à dire si elles peuvent modéliser une situation "supermarché". Prenons la fonction g:
g(0) = 2
Alors tu rentres dans un supermarché, tu achètes "0 kilos" (donc rien du tout).. et dois payer 2 euros quand même. Est-ce que c'est une situation de proportionnalité ?
Si on veut l'écrire plus mathématiquement, on doit disposer d'un unique nombre "a" fixé (qui est donc le coefficient dont je t'ai parlé) tel que g s'écrive: g(x) = a*x pour tout nombre x
Mais g(4) = 4, donc a*4 = 4 donc a = 1
Et g(5) = 3, donc a*5 = 3, donc a = 3/5
Donc ce nombre a unique n'existe pas puisqu'il est différent selon le x que tu choisis.... On est en train de multiplier chaque x par un truc différent et donc g ne peut être linéaire !
Pour f, la situation est différente. Regardons. Supposons que f(x) = m*x (avec m un nombre fixé)
f(2) = 3
donc 2*m = 3 donc m = 3/2
Mais aussi f(4) = 6
donc m*4 = 6, donc m = 6/4 = 3/2
Si tu fais avec toutes les valeurs du tableau, tu vas trouver toujours m = 3/2, donc f est bien une fonction linéaire. En effet, c'est un tableau de proportionnalité: tu achètes x kilos, tu payes 3/2*x euros. C'est logique.
Alors que pour g, ce n'est pas le cas: tu peux acheter 4 kilos et payer 4 euros, ne rien acheter et payer 2 euros... c'est pas de la proportionnalité.
En ce qui concerne ton exercice 2, c'est une bonne approche que tu as, mais tu utilises la même lettre pour désigner une fonction linéaire "f" (tu devrais/aurais du changer la notation parce que ce sont des fonctions différentes avec des coefficients différents).
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Fonctions linéaires.
Oh, je vois. Merci beaucoup. Votre explication m'aidera non seulement pour faire cet exercice, mais à comprendre tous les exercices sur lesquels je peux tomber sans être prise de panique sous prétexte d'avoir un objet mathématique mystérieux, compliqué et qui viole la beauté des mathématiques face à moi..
Merci encore. Je vais noter vos explications dans mon cahier des maths de sorte que je trouve des formules simplifiées qui résument toute la leçon quand j'aurai besoin de résoudre un exo.
D'accord Lostounet, je prends votre remarque en note. Merci infiniment.
Bonne soirée !
Merci encore. Je vais noter vos explications dans mon cahier des maths de sorte que je trouve des formules simplifiées qui résument toute la leçon quand j'aurai besoin de résoudre un exo.
D'accord Lostounet, je prends votre remarque en note. Merci infiniment.
Bonne soirée !
Re: Fonctions linéaires.
Si jamais tu as d'autres questions n'hésite pas, même sur des bases!
J'espère avoir été suffisamment clair.
J'espère avoir été suffisamment clair.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
