Dériver une intégrale

[FunkyAnts]

Bonsoir,

j'ai besoin de votre aide pour me lancer dans un exo.

On me demande de dériver une 1ere fois puis une 2eme fois G(x).

Avec G(x)=

Et je ne connais pas la méthode. Et dans mon cours il n'y a pas d'exemples de ce type. Est-ce que je dois d'abord calculer l'intégrale (de 0 à x) puis la dériver 2 fois ? Ou existe t-il une méthode plus simple ?

Merci.

[BiancoAngelo]

Bonsoir,

j'ai besoin de votre aide pour me lancer dans un exo.

On me demande de dériver une 1ere fois puis une 2eme fois G(x).

Avec G(x)=

Et je ne connais pas la méthode. Et dans mon cours il n'y a pas d'exemples de ce type. Est-ce que je dois d'abord calculer l'intégrale (de 0 à x) puis la dériver 2 fois ? Ou existe t-il une méthode plus simple ?

Merci.

Bonsoir !

Oui il y a plus simple, car on ne peut pas systématiquement trouver une primitive.
Mais par contre, on sait que des primitives existent.

Donc, posons F une primitive de la fonction f définie par .

Alors .

Donc (car F primitive de f).

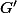
Et après tu dérives facilement...

[FunkyAnts]

Merci BiancoAngelo.