Salut à tous,
je cherche à calculer la limite vers +∞ de ce polynôme :
√(x^2 )- √(x^2 + x)
comme c'est un cas indéterminé (+∞ - ∞), et que c'est une forme de type a - b, on utilise la méthode du conjugué (d'après ce que j'ai appris), donc :
lim √(x^2 )- √(x^2 + x)
= lim [[√(x^2 )- √(x^2 + x)][√(x^2 )+ √(x^2 + x)]] / √(x^2 )+ √(x^2 + x)
ensuite on a par la distribution :
[ x^2 + [√(x^2 )*√(x^2 + x)] - [√(x^2 )*√(x^2 + x)] - (x^2 + x) ] / √(x^2 )+ √(x^2 + x)
les termes en rouge s'annulent.
On a donc :
x^2 - x^2 - x / √(x^2 )+ √(x^2 + x)
= - x / √(x^2 )+ √(x^2 + x)
= - x / √[x(2x+1)]
Si je n'ai pas fait d'erreur(s) jusque là, quelqu'un sait comment finir le calcul de cette limite ? J'avoue ne pas être très à l'aise avec cette racine, que je ne maîtrise pas encore.
Merci d'avance !
Analyse 1 : Limites vers l'infini (EPFL)
6 messages
- Page 1 sur 1
Re: Analyse 1 : Limites vers l'infini (EPFL)
Où ça un polynôme ?
Il ne faut pas prendre des vessies pour des lanternes.
Tu fais comme si ??????
??????
Et par ailleurs, la première fraction n'est pas parenthésée convenanblement.
Remarque : pour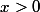 , on a
, on a  .
.
Il ne faut pas prendre des vessies pour des lanternes.
- x / √(x^2 )+ √(x^2 + x) = - x / √[x(2x+1)]
Tu fais comme si
Et par ailleurs, la première fraction n'est pas parenthésée convenanblement.
Remarque : pour
Re: Analyse 1 : Limites vers l'infini (EPFL)
Manque d'attention effectivement, toutes mes excuses, je parlais donc de la fonction :
a(x) = √(x^2 )- √(x^2 + x)
Pour ce qui est des racines, mon amie et moi n'étions pas très sûres mais en y repensant c'est complètement idiot aha car √2 + √2 n'est pas égal à √4... il faudra entraîner tout ça aha
Pardon pour cette confusion, ça doit être difficile de me suivre :
(x^2 - x^2 - x )/ [√(x^2 )+ √(x^2 + x)]
= - x / [√(x^2 )+ √(x^2 + x)]
= - x / √[x(2x+1)]
pour le √x^2, j'en étais convaincue mais je me suis laissée convaincre du contraire par mon groupe... :s
Merci pour tes corrections Robot, je vais tenter de trouver cette limite à présent:)
a(x) = √(x^2 )- √(x^2 + x)
Pour ce qui est des racines, mon amie et moi n'étions pas très sûres mais en y repensant c'est complètement idiot aha car √2 + √2 n'est pas égal à √4... il faudra entraîner tout ça aha
Pardon pour cette confusion, ça doit être difficile de me suivre :
(x^2 - x^2 - x )/ [√(x^2 )+ √(x^2 + x)]
= - x / [√(x^2 )+ √(x^2 + x)]
= - x / √[x(2x+1)]
pour le √x^2, j'en étais convaincue mais je me suis laissée convaincre du contraire par mon groupe... :s
Merci pour tes corrections Robot, je vais tenter de trouver cette limite à présent:)
Re: Analyse 1 : Limites vers l'infini (EPFL)
DetGirl8 a écrit:- x / [√(x^2 )+ √(x^2 + x)] = - x / √[x(2x+1)]
Non, mais je rêve ??
Re: Analyse 1 : Limites vers l'infini (EPFL)
Vous avez écrit :
= - x / [√(x^2 )+ √(x^2 + x)]
= - x / √[x(2x+1)]
que j'écrirai comme ça :

}})
L'erreur que vous avez faite, je l'ai faite souvent dans le passé :
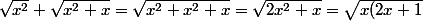})
en général et par conséquent
et par conséquent 
donc}} = - \frac{x}{\sqrt{x^2} + \sqrt{x^2} \sqrt{1 + \frac{1}{x}}})
de là vous pouvez continuer et conclure .
= - x / [√(x^2 )+ √(x^2 + x)]
= - x / √[x(2x+1)]
que j'écrirai comme ça :
L'erreur que vous avez faite, je l'ai faite souvent dans le passé :
en général
donc
de là vous pouvez continuer et conclure .
Re: Analyse 1 : Limites vers l'infini (EPFL)
Merci infiniment aymanemaysae ! ça m'aide beaucoup 
Désolée Robot, je ne suis vraiment pas à l'aise avec ces racines :s
Désolée Robot, je ne suis vraiment pas à l'aise avec ces racines :s
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
