ANNEAU (MATHS FONDAMENTALES)

[Kajania]

Soit (A, +, x) un anneau commutatif (par exemple A := Z). On désigne par P l'ensemble des suites (aj)[size=85]j≥0[/size] de A nulles à partir d'un certain rang, c'est-à-dire qu'il existe un entier n ≥ 0 tel que aj = 0 pour j ≥ n + 1. Si P := (aj)j≥0 et Q := (bj)j≥0 sont des éléments de P on définit leur addition et leur multiplication par
- P + Q := (aj + bj)j≥0
- PQ := (cj)j≥0 où cj := ∑ aibk = ∑ aibj-i
1) Vérifier que (P, +, x) est un anneau commutatif. Montrer que e:= (ej)j≥0 où e0:= 1 et ej:= 0 pour j ≥ 1 est un élément neutre pour la multiplication.
2) On pose X:= (0, 1, 0, 0, …) l'élément de P qui a tous ses éléments nuls pour tous les indices j ≥ 2. calculer X², X3 et en déduire la forme générale de l'élément Xn.
3) Vérifier que tout élément P = (aj)j≥0 ϵ P s'écrit de manière unique, pour un entier n que l'on décrira, P = ∑ akXk.
4) Vérifier que si (A, +, x) est un corps (par exemple A:= R), on peut munir, de manière naturelle, P d'une structure d'espace vectoriel sur A.

[Ben314]

Salut,
Tu as fait quoi ?
Tu bloque où ?

[Kajania]

Je bloque dès le début (désolé je débute tout juste les maths fondamentaux).
Par exemple pour prouver que c'est un anneau commutatif, je ne vois pas quelle fonction prendre. J e ne vois pas comment retranscrire "les suites (aj) de A nulles à partir d'un certain rang"

[Ben314]

Je comprend pas ce que tu raconte : c'est quoi la fonction f que tu "voudrait prendre" ?
Qu'est ce que tu veut dire par "retranscrire" que la suite (aj) est nulle a partir d'un certain rang ?

Dans un exo. de ce style, le seul truc à faire, c'est de regarder la définition de ce qu'est un anneau commutatif (unitaire je suppose) et de vérifier un par un que tout les trucs de la définition en question sont vérifiés dans le cas de l'ensemble P muni des deux loi + et x qu'on te donne.

C'est quoi le(s) premier(s) trucs à vérifier ?

[Kajania]

J'ai finalement réussi la une en répondant à chaque propriétés de l'anneau commutatif.
Maintenant je bloque sur la 2 je sais pas comment m'y prendre

[Ben314]

Tu peut préciser ce que tu as montré pour la 1) histoire de vérifier que tout y est ? (il est très facile d'oublier des trucs dans un cas pareil...)

Pour le 2), c'est on ne peut plus simple : que donne la définition du produit PxQ qu'on te donne dans le cas où P=X=(0,1,0,0,0,...) et Q=X=(0,1,0,0,0,0,...) ? (c'est évidement ce produit XxX qui est noté X²)
Ensuite, que donne la définition du produit PxQ lorsque P=X=(0,1,0,0,0,...) et Q=X²=(ce que tu as trouvé précédemment) ?
etc...

Par contre, pour la question 3), il te manque une définition pour pouvoir répondre de façon "carrée" à la question : on y parle de ak x X^k qui est le produit d'un élément de A avec un élément de P alors qu'un tel produit n'a pas été défini par l'énoncé.
A ton avis, c'est quoi la définition d'un tel produit ? (plusieurs réponse possible qui, heureusement, donnent le même résultat)

[Kajania]

pour la 1 j'ai montré:
- + et x sont des lois de composition interne sur P
- (P, +)est un groupe commutatif (ou abélien)
- x est associative dans P
- x est distributive par rapport à +

[Kajania]

pour la 2:
(0, 1, 0, 0, ...) x (0, 1, 0, 0, ...) = (0, 1, 0, 0, ...) ?

[Ben314]

pour la 1 j'ai montré:
- + et x sont des lois de composition interne sur P
- (P, +)est un groupe commutatif (ou abélien)
- x est associative dans P
- x est distributive par rapport à +

C'est (quasi) bon.
Ici, LE truc à ne pas oublier, c'est de montrer que ce sont des loi de composition internes, c'est à dire que la somme ainsi que le produit de deux éléments de P et bien dans P : c'est pas trop compliqué pour la somme, mais un peu plus technique pour le produit si on ne sait pas par quel bout s'y prendre.

Mais il te manque quelques trucs :
- Comme on te demande de montrer que c'est un anneau commutatif, il faut montrer que est commutatif.
- Vérifie dans ton cours, mais pour de nombreux auteurs, un anneau doit forcément être unitaire (sinon on parle de "pseudo anneau") et, évidement, dans ce cas, il faut aussi montrer que admet un élément neutre.

(0, 1, 0, 0, ...) x (0, 1, 0, 0, ...) = (0, 1, 0, 0, ...) ?

Perdu... Try again...

[Kajania]

je vois vraiment pas pour la 2, on doit s'y prendre comme pour des vecteurs ?

[Kajania]

(0, 1, 0, 0,... ) x (0, 1, 0, 0,...) = (0, 0, 0, 0 + 0, 1, 0, 0 + 0, 0, 0, 0 + 0, 0, 0, 0 + ...)

[Kajania]

(0, 1, 0, 0,... ) x (0, 1, 0, 0,...) = (0, 0, 0, 0,... + 0, 1, 0, 0,... + 0, 0, 0, 0,... + 0, 0, 0, 0,... + ...) ?

[Kajania]

pour la 4 puis-je utiliser ceci :
On dit que l’ensemble E est un espace vectoriel sur K (ou encore un K-espace vectoriel) si :
– l’ensemble E est muni d’une loi interne + pour laquelle il a une structure de groupe commutatif.
– Il existe une application (α, u) → αu de K × E dans E, dite loi externe, telle que :
pour tous scalaires α et β et pour tous éléments u, v de E
(α + β)u = αu + βu, α(u + v) = αu + αv
α(βu) = (αβ)u, 1u = u

[Ben314]

Si P := (aj)j≥0 et Q := (bj)j≥0 sont des éléments de P
- PQ := (cj)j≥0 où cj := ∑ aibk = ∑ aibj-i

Si P=Q=(0,1,0,0,0,0,...), c'est à dire si aj=bj=0 sauf a1=b1=1, combien valent les différents cj := ∑ aibk = ∑ aibj-i ?

J'ai du mal à comprendre comment tu as fait pour montrer par exemple que le produit était interne dans P ou bien qu'il était associatif sachant que, visiblement, tu ne comprend pas comment appliquer la définition de ce même produit dans un cas excessivement élémentaire...

[Ben314]

pour la 4 puis-je utiliser ceci :
On dit que l’ensemble E est un espace vectoriel sur K (ou encore un K-espace vectoriel) si :
– l’ensemble E est muni d’une loi interne + pour laquelle il a une structure de groupe commutatif.
– Il existe une application (α, u) → αu de K × E dans E, dite loi externe, telle que :
pour tous scalaires α et β et pour tous éléments u, v de E
(α + β)u = αu + βu, α(u + v) = αu + αv
α(βu) = (αβ)u, 1u = u

Oui, sauf que si tu explique pas qui c'est la fameuse "loi externe" en question, ben on peut pas dire que tu ait montré quoi que ce soit...

[Kajania]

je comprends toujours pas pour la 2 désolé
et pour la 4 comment peut-on montré la loi externe ?

[Ben314]

Si pour tout sauf alors
et, pour tout , .

Donc, si tout les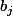 sont nuls sauf 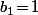alors tout les 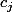sont nuls sauf ce qui signifie que

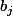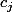De même, si tout les sont nuls sauf alors tout les sont nuls sauf ce qui signifie que

etc...

Sinon, autant je comprend parfaitement ce que signifie "montrer une propriété", autant il faudrait que tu m'explique ce que tu entend par "montrer une loi" pour que je réponde à ta question.

Bref, il faut que tu trouve (ou que tu invente, ou que tu définisse) une loi externe sur P puis il faut que tu montre (ou que tu démontre ou que tu prouve ou que tu justifie) que la loi que tu as posé/définie/inventé vérifie bien les propriétés demandés pour que (P,+, . ) soit effectivement un espace vectoriel sur le corps A.

A ton avis, si sont dans , on va prendre quoi comme définition de ?

[Kajania]

Pourriez vous m'aider pour la 3 svp ?