Soit la définition suivante:
où
Alors est-ce que le résultat ci-dessous est correct?
et
Donc
et
Sinus et cosinus en des angles particuliers
8 messages
- Page 1 sur 1
sinus et cosinus en des angles particuliers
par 0bjective » 04 Mar 2016, 16:40
Bonjour,
Soit la définition suivante:
 \\= \sum_{n=0}^{\infty} 2(\frac{-1}{2})^n \vec{R}_n(\theta) \\= R_y(\theta)\vec{u} + R_x(\theta)\vec{v})
où
 = cos(n\theta)\vec{u} - sin(n\theta)\vec{v})
et
 = \sum_{n=0}^{\infty} 2(\frac{-1}{2})^n cos (n\theta))
 = -\sum_{n=0}^{\infty} 2(\frac{-1}{2})^n sin (n\theta))
et 
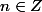
Alors est-ce que le résultat ci-dessous est correct?
 \\= \sum_{n=0}^{\infty} 2(\frac{-1}{2})^n \frac{1}{2}((-i)^n + i^n) \\= \sum_{n=0}^{\infty} (\frac{-1}{2})^n ((-i)^n + i^n) \\= 2(\frac{1}{2^0} - \frac{1}{2^2}+\frac{1}{2^4}-\frac{1}{2^6}+\frac{1}{2^8}-... ) \\= 2\sum_{n=0}^{\infty} (\frac{-1}{2^2})^n)
et
 \\= \sum_{n=0}^{\infty} -2(\frac{-1}{2})^n \frac{i}{2}((-i)^n - i^n) \\= -\sum_{n=0}^{\infty} (\frac{-1}{2})^n i((-i)^n - i^n) \\= 2(\frac{1}{2^1} - \frac{1}{2^3}+\frac{1}{2^5}-\frac{1}{2^7}+\frac{1}{2^9}-... )\\= 2\sum_{n=0}^{\infty}\frac{(-1)^n}{2^{2n+1}}=\sum_{n=0}^{\infty} (\frac{-1}{2^2})^n \\= \frac{R_y}{2})
Donc
 = \vec{u} +\frac{1}{2}\vec{v})
et
 = (\vec{u} + \frac{1}{2}\vec{v})\sum_{n=0}^{\infty} (\frac{-1}{2^2})^n)
?
Soit la définition suivante:
où
Alors est-ce que le résultat ci-dessous est correct?
et
Donc
et
Re: sinus et cosinus en des angles particuliers
par Ben314 » 04 Mar 2016, 17:00
ça a l'air bon, mais tant qu'à faire de manipuler des nombres complexes, partant de ça :
 = 2\sum_{n=0}^{\infty} (-\frac{1}{2})^n \cos (n\theta))
;  = -2\sum_{n=0}^{\infty} (-\frac{1}{2})^n \sin (n\theta))
Tu peut écrire que :
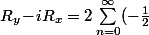^n \big(\cos(n\theta)\!+\!i\sin(n\theta)\big))
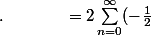^ne^{ni\theta}=2\sum_{n=0}^{\infty} (-\frac{1}{2}e^{i\theta})^n)
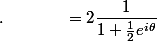
car, si 
alors 
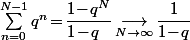
\!-\!i\sin(\theta)}{5+4\cos(\theta)})
Donc}{5+4\cos(\theta)})
et \big)}{5+4\cos(\theta)})
Et, en particulier, pour
, ça donne 
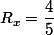
et 
Tu peut écrire que :
Donc
Et, en particulier, pour
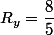
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: sinus et cosinus en des angles particuliers
par 0bjective » 04 Mar 2016, 17:40
Salut Ben314,
merci beaucoup, cela donne en effet les mêmes résultats qu'avec ma méthode:
https://www.google.be/search?newwindow= ... BuVDKz6Vvo
Excellent! une tout grand merci pour cette confirmation!
merci beaucoup, cela donne en effet les mêmes résultats qu'avec ma méthode:
https://www.google.be/search?newwindow= ... BuVDKz6Vvo
Excellent! une tout grand merci pour cette confirmation!
Re: sinus et cosinus en des angles particuliers
par 0bjective » 04 Mar 2016, 18:58
Mais donc juste pour être sûr d'avoir bien compris :
pour
:
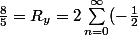^n \cos (n\pi/2))
Mais c'est également :
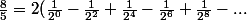 = 2\sum_{n=0}^{\infty} (-\frac{1}{2})^n)
où)
a disparu magiquement...où a-t-il disparu???
Que peut-on conclure?
pour
Mais c'est également :
où
Que peut-on conclure?
Re: sinus et cosinus en des angles particuliers
par Ben314 » 04 Mar 2016, 19:30
La suite \big)_{n\geq 0})
c'est tout bêtement la suite )
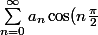donc =a_0-a_2+a_4-a_6+a_8\cdots)
pour n'importe quelle suite _{n\geq 0})
.
En particulier,
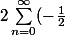^n\cos(n\frac{\pi}{2})=2\Big((-\frac{1}{2})^0-(-\frac{1}{2})^2+(-\frac{1}{2})^4-(-\frac{1}{2})^6+\cdots\Big)=2\Big(1-\frac{1}{2^2}+\frac{1}{2^4}-\frac{1}{2^6}+\cdots\Big)=2\sum_{n=0}^\infty (-\frac{1}{2^2})^n)
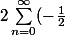Mais qui n'est pas égale à^n)
.
En particulier,
Mais qui n'est pas égale à
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: sinus et cosinus en des angles particuliers
par 0bjective » 04 Mar 2016, 21:13
Ok encore une fois merci Ben134 (j'avais oublié)
Mais donc pour :
^n \cos (n\pi/2)=2\sum_{n=0}^{\infty} (-\frac{1}{2^2})^n \\ =2\sum_{n=0}^{\infty} (-\frac{1}{2})^n (\frac{1}{2})^n)
Donc
 = (\frac{1}{2})^n)
? Ce n'est pas logique...
Il y a toujours quelquechose qui m'échappe...Je ne comprends pas
mais ça doit être tout bête...
Mais donc pour
Donc
Il y a toujours quelquechose qui m'échappe...Je ne comprends pas
mais ça doit être tout bête...
Re: sinus et cosinus en des angles particuliers
par Ben314 » 04 Mar 2016, 21:46
La suite (-\frac{1}{2})^n\big)_{n\geq 0})
c'est )
La suite^n\big)_{n\geq 0})
c'est )
Les sommes des deux suites sont les mêmes, mais ce ne sont pas les même termes : le
-ième terme (en commençant à 0) de la deuxième suite c'est le 
-ième terme de la première.
Bilan : tu n'as pas^n=\cos(n\frac{\pi}{2})(-\frac{1}{2})^n)
, mais par contre tu as bien ^n=\cos(2n\frac{\pi}{2})(-\frac{1}{2})^{2n})
.
La suite
Les sommes des deux suites sont les mêmes, mais ce ne sont pas les même termes : le
Bilan : tu n'as pas
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: sinus et cosinus en des angles particuliers
par 0bjective » 04 Mar 2016, 23:17
Ben314 a écrit:Bilan : tu as bien
Autrement dit:
Donc
Merci beaucoup Ben134, tu as réponse à tout!
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :