DM de Math de BTS

[zozo42]

Bonjour,

Je m'appelle Zoé je suis actuellement en 1ere année de BTS et j'ai eu un DM de math a faire et il y a 5 questions que je n'arrive pas du tout a faire, pourriez vous m'aider ??

Merci d'avance.

voici les 5 questions et les réponse proposé par l'énoncer:
1)Un algorithme commence avec deux variables X et Y. Ces variables sont des nombres entiers.



Donner en fonction de X et Y la valeur affichée finale.



Algorithme

---------------

Saisir X

Saisir Y

X <- X+Y
Y <- X-Y
X <- X-Y
X <- X+Y
Y <- X+Y

Afficher ("Première variable=",X,"Seconde variable=",Y)

les réponse possible:
L'affichage final est :

Première varaible=Y, Seconde variable=X


L'affichage final est :

Première varaible=3X+Y, Seconde variable=2X


L'affichage final est :

Première varaible=2X, Seconde variable=2X+Y


L'affichage final est :

Première varaible=2X, Seconde variable=3X


L'affichage final est :

Première varaible=3X, Seconde variable=X+Y



2)Un programme en Python doit afficher le prix d'un article de boulangerie en entrant sa dénomination.

La liste des prix est :

Baguette 0,82 E

Croissant à,75E

Brioche 4 euros

Tarte au myrtilles 8E



Programme en Python

-------------

prix=0

T=[["Baguette","Croissant","Brioche","Tarte aux myrtilles"],[0.82,0.75,4,8]]

prod=input("Entrer l'article")

#completer

#-----------

#------------

Print("Le prix est ", prix,"E")



Completer la partie manquante par le pseudo code suivant

qui traduit en Python donnerait le bon résulatat.

Programma Python

Les réponses possible:
Pour i allant de 1 à 4

si T[i]=T[i+1] alors prix=T[I+1]






Pour i allant de 1 à 4

si T[i][j]=T[j][i} alors prix=T[j][i]


Pour i allant de 0 à 3

si prod=T[0][i] alors prix=T[1][i]


Pour i allant de 1 à 4

Pour j allant de 1 à 4

si prod=T[i][j] alors prix=T[1][i]


Pour i allant de 1 à 4

si prod=T[0][i] alors prix=T[1][i]


3)Un algorithme saisi trois entiers posiifs, les déposent dans deux variables X et Y, puis effectue une série de calculs en utilisant une boucle.

Afficher ("Saisir trois entier positifs")

Saisir (X)
Saisir (Y)
Si X+Y<1
Saisir (X)
Saisir (Y)
Z=0
Fin si
Pour i allant de 1 a N
Pour J allant de 1 a X+Y
Z <- z+X-Y
Fin de boucle pour J
fin de boucle pour I
Afficher (Z)

Dans le cas ou l'on a rentré un entier n positif et deux autres entiers X, Y tels que X+Y>=1, on obtient en affichahe final les valeurs suivantes

Les réponses possibles:
n(X+Y)


nX-nY+n²


n(X+Y)^3


n(X+Y)²


nX²-nY²



4)Le même programme en python comporte 5 commentaires differents.

Retrouver l'unique programme bien commenté suivant.

réponses possibles:

Programme1:
#Le programme suivant demande un entier puis donne la #liste de tous ses diviseurs classés par ordre croissant, puis #la liste des facteurs premiers et leur puissances #respectives
from math import sqrt #importation de la fonction racine
n=long(input("Entrer le nombre"))
T=[] #tableau des diviseurs
S=[] #tableau des facteurs premiers initialisés avec des "0"
m=0
c=0
for i in range(1, long(sqrt(n))+1): #On ne teste les diviseurs # qu entre 1 et racine(n)+1
if (n%i==0): #On teste si n est bien un diviseur
T.append(i) #On range le diviseur dans le tableau
T.append(n/i) #On range aussi le diviseur #complementaire

if (len(T)==2): #Si n est premier on trouve 2 diviseurs 1 et #l'entier n
print(n," est premier")
else:
T.sort() #Tri des diviseurs
print("Les diviseurs de ",n," sont:")
print(T) #Affiche tous les diviseurs dans l'ordre

for i in range(1,len(T)): #On parcourt le tableau des diviseurs
c=2 #On commence à diviser par 2
m=long(sqrt(T[i])+1) #Si il n'existe aucun diviseur < #racine(n)+1 alors n est premier
while (T[i]%c!=0 and c<=m): #on teste si c est diviseur
c+=1
if (c>m): #On teste si le diviseur est premier
S.append(T[i])
if (T[i]==2): # 2 est premier et valeur entiere de (racine #(2)+1)=2
S.append(T[i])
print("Les facteurs premiers (sans leurs puissances) de ",n," sont:")
print(S) #Affiche les facteur premiers

Programme2:



#Le programme suivant demande un entier puis donne la #liste de tous ses diviseurs classés par ordre croissant, #puis la liste des facteurs premiers
from math import sqrt #importation de la fonction racine
n=long(input("Entrer le nombre"))
T=[] #tableau des diviseurs initialisé vide
S=[] #tableau des facteurs premiers
m=0
c=0
for i in range(1, long(sqrt(n))+1): #On ne teste les #diviseurs qu entre 1 et racine(n)+1
if (n%i==0): #On teste si i est bien un diviseur
T.append(i) #On range le diviseur dans le #tableau
T.append(n/i) #On range aussi le diviseur #complementaire

if (len(T)==2): #Si n est premier on trouve 2 diviseurs 1 et #l'entier n
print(n," est premier")
else:
T.sort() #Tri des diviseurs
print("Les diviseurs de ",n," sont:")
print(T) #Affiche tous les diviseurs dans l'ordre

for i in range(1,len(T)): #On parcourt le tableau des #diviseurs
c=2 #On commence à diviser par 2
m=long(sqrt(T[i])+1) #Si il n'existe aucun diviseur < #racine(n)+1 alors n est premier
while (T[i]%c!=0 and c<=m):
c+=1
if (c>m): #On teste si le diviseur est premier
S.append(T[i])
if (T[i]==2): # 2 est premier et valeur entiere de #(racine(2)+1)=2
S.append(T[i])
print("Les facteurs premiers (sans leurs puissances) de ",n," sont:")
print(S) #Affiche les facteur premiers

Programme3:
#Le programme suivant demande un entier puis donne la #listede tous ses diviseurs classés par ordre décroissant; #puis la liste des facteurs premiers
from math import sqrt #importation de la fonction #racine
n=long(input("Entrer le nombre"))
T=[] #tableau des diviseurs
S=[] #tableau des facteurs premiers
m=0#constante servant a compter les diviseurs
c=0
for i in range(1, long(sqrt(n))+1): #On ne teste les #diviseurs qu entre 1 et racine(n)+1
if (n%i==0): #On teste si n est bien un diviseur
T.append(i) #On range le diviseur dans le tableau
T.append(n/i) #On divise par n par i

if (len(T)==2): #Si n est premier on trouve 2 diviseurs 1 et #l'entier n
print(n," est premier")
else:
T.sort() #Tri des diviseurs
print("Les diviseurs de ",n," sont:")
print(T) #Affiche tous les diviseurs dans l'ordre

for i in range(1,len(T)): #On parcourt le tableau des #diviseurs
c=2 #On commence à diviser par 2
m=long(sqrt(T[i])+1) #Si il n'existe aucun #diviseur < #racine(n)+1 alors n est premier
while (T[i]%c!=0 and c<=m):
c+=1
if (c>m): #On recherche des diviseurs
S.append(T[i])
if (T[i]==2): # 2 est premier et valeur entiere de #(racine #(2)+1)=2
S.append(T[i])
print("Les facteurs premiers (sans leurs puissances) de ",n," sont:")
print(S) #Affiche les facteur premiers et leurs puissances

Programme4:


#Le programme suivant demande un entier puis donne la #liste de tous ses diviseurs classés par ordre croissant, puis #la liste des facteurs premiers
from math import sqrt #importation de la fonction #racine
n=long(input("Entrer le nombre"))
T=[] #tableau des diviseurs initialisé vide
S=[] #tableau des facteurs premiers
m=0
c=0
for i in range(1, long(sqrt(n))+1): #On ne teste les #diviseurs qu entre 1 et racine(n)+1
if (n%i==0): #On teste si i est bien un diviseur
T.append(i) #On range le diviseur dans le tableau
T.append(n/i) #On range aussi le diviseur #complémentaire même si il n est pas diviseur de n

if (len(T)==2): #Si n est pas premier on trouve 2 diviseurs #1 et l'entier n
print(n," est premier")
else:
T.sort() #Tri des diviseurs
print("Les diviseurs de ",n," sont:")
print(T) #Affiche tous les diviseurs dans l'ordre

for i in range(1,len(T)): #On parcourt le tableau des #diviseurs
c=2 #On commence à diviser par 2
m=long(sqrt(T[i])+1) #Si il n'existe aucun diviseur < #racine(n)+1 alors n est premier
while (T[i]%c!=0 and c<=m):
c+=1
if (c>m): #On teste si le diviseur est premier
S.append(T[i])
if (T[i]==2): # 2 est premier et valeur entiere de (racine #(2)+1)=2
S.append(T[i])
print("Les facteurs premiers (sans leurs puissances) de ",n," sont:")
print(S) #Affiche les facteur premiers

Programme5:
#Le programme suivant demande un entier puis donne la #liste de tous ses diviseurs classés , puis la liste des #facteurs premiers
from math import sqrt #importation de la fonction racine
n=long(input("Entrer le nombre"))
T=[] #tableau des diviseurs initialisé vide
S=[] #tableau des facteurs premiers initialisé vide
m=0
c=0
for i in range(1, long(sqrt(n))+1): #On ne teste les diviseurs #qu entre 1 et racine(n)+1
if (n%i==0): #On teste si n est bien un diviseur
T.append(i) #On range le diviseur i dans le début du #tableau T
T.append(n/i) #On divise par i

if (len(T)==2): #Si n n'est pas premier on trouve 2 diviseurs #1 et l'entier n
print(n," est premier")
else:
T.sort() #Tri des diviseurs
print("Les diviseurs de ",n," sont:")
print(T) #Affiche tous les diviseurs dans l'ordre

for i in range(1,len(T)): #On parcourt le tableau des #diviseurs
c=2 #On commence à diviser par 2
m=long(sqrt(T[i])+1) #Si il n'existe aucun diviseur < #racine(n)+1 alors n est premier
while (T[i]%c!=0 and c<=m):
c+=1
if (c>m): #On teste si le diviseur est premier
S.append(T[i])
if (T[i]==2): # 2 est premier et valeur entiere de (racine #(2)+1)=2
S.append(T[i])
print("Les facteurs premiers (sans leurs puissances) de ",n," sont:")
print(S) #Affiche les facteur premiers


5)Un même programme a été commenté de plusieurs manières différentes. Donner le commentaire qui ne comporte pas d'erreurs.

Réponse possibles:
Programme1:
#Le programme demande d'entrer deux entiers n1 #et n2 (n1>n2) puis
#recherche les facteurs premiers de tous les #nombres compris dans l'intervalle [n1,n2]
from math import sqrt #importation de la #fonction racine carrée
#------------------------------
n1,n2=2,1 #initialisation pour entrer dans la #boucle
while (n1>n2): #Redemande la saisie des deux #nombres si (n1>n2)
n1=int(input("Entrer le pemier entier positif "))
n2=int(input("Entrer un second entier positif supérieur "))
print("Voici la décomposition en facteurs premiers des entiers entre ",n1," et ", n2)
#----------------------
T=[] #tableau à une dimensions pour stockage des #nombres et de leurs facteurs premiers
S=[] #tableau unidimensionnel pour stockage des #nombres premiers utiles
m=0
#--------------------
for i in range(0,n2-n1+1):
T.append([]) #crée le tableau à deux #dimensions vide
#---------------------
HH=range(3,int(sqrt(n2))+1)
c=0 #initialisation d'un compteur
S.append(2)
for i in HH: #Boucle pour la recherche des #nombres premiers plus grand que racine(n2)+1
m=int(sqrt(i))+1
c=2
while (c<=m and i%c!=0):
c+=1
if (c>m): #Teste si le nombre est premier
S.append(i) #Stocke le nombre premier

#----------------------------------
HH=range(n1,n2+1)
for i in HH: #Boucle principale faisant varier #les valeurs dans l'intervalle [n1,n2}
T[i-n1].append(i) # valeur de l'entier stocké en #indice 0
c=0 #Initialisation du compteur
m=len(S)-1 #nombre premier
nb=i
while(c<=m and nb>1):
while (nb%S[c]==0): #Tant que S[c] est un #diviseur on divise nb par S[c]
nb=nb/S[c]
T[i-n1].append(S[c]) #on stocke le diviseur
c=c+1
if (nb!=1):
T[i-n1].append(nb) #Stocke l'unique facteur #plus grand que racine(i)+1 ou la valeur i si i est #premier

#-------------------------------------
for i in range(0,n2-n1+1):
if len(T[i])==2:#Teste si le nombre est premier, #dans ce cas on a deux diviseurs 1 et i
print("------------------")
print("Le nombre ",T[i][0],"est premier") #T[i][0] est le nombre lui meme.
print("------------------")
else:
print("Liste des facteurs premiers de ",i+n1)
print(T[i][1:len(T[i])]) #Affiche tous les #facteurs premiers(l'indice 0 qui est l'entier n'est #pas affiché)


Programme2:
#Le programme demande d'entrer deux entiers n1 #et n2 (n2>n1) puis
#recherche les facteurs premiers de tous les #nombres compris dans
#l'intervalle [n1,n2]
from math import sqrt #importation de la #fonction racine carrée
#------------------------------
n1,n2=2,1
while (n1>n2): #Redemande la saisie des deux #nombres si (n1>n2)
n1=int(input("Entrer le pemier entier positif "))
n2=int(input("Entrer un second entier positif supérieur "))
print("Voici la décomposition en facteurs premiers des entiers entre ",n1," et ", n2)
#----------------------
T=[] # Liste demeurant un tableau à une #dimension pour stockage des nombres et de leurs
# facteurs sans le 1
S=[] #tableau unidimensionnel pour stockage des # nombres premiers utiles
m=0
#--------------------
for i in range(0,n2-n1+1):
T.append([]) #crée un tableau à une #dimensions vide
#---------------------
HH=range(3,int(sqrt(n2))+1)
c=0 #initialisation d'un compteur
S.append(2)
for i in HH: #Boucle pour la recherche des #nombres premiers plus petit que racine(n2)+1
m=int(sqrt(i))+1
c=2 #Commencer par le diviseur 1 n'est pas #utile
while (c<=m and i%c!=0):
c+=1
if (c>m): #Teste si le nombre est premier
S.append(i) #Stocke le nombre premier

#----------------------------------
HH=range(n1,n2+1)
for i in HH: #Boucle principale faisant varier #les valeurs dans l'intervalle [n1,n2}
T[i-n1].append(i) # valeur de l'entier stocké en #indice i
c=0 #Initialisation du compteur
m=len(S)-1 #indice du premier nombre premier #stocké dans le tableau S
nb=i
while(c<=m and nb>1):
while (nb%S[c]==0): #Tant que S[c] est un #diviseur on divise nb par S[c]
nb=nb/S[c]
T[i-n1].append(S[c]) #on stocke le diviseur
c=c+1
if (nb!=1):
T[i-n1].append(nb)

#-------------------------------------
for i in range(0,n2-n1+1):
if len(T[i])==2:#Teste si le nombre est premier #(T[i][0]=n )
print("------------------")
print("Le nombre ",T[i][0],"est premier") #T[i][0] est le nombre lui meme.
print("------------------")
else:
print("Liste des facteurs premiers de ",i+n1)
print(T[i][1:len(T[i])]) #Affiche tous les #facteurs premiers(l'indice 1 qui est l'entier n'est #pas affiché)


Programme3:


#Le programme demande d'entrer deux entiers n1 #et n2 (n2>n1) puis
#recherche les facteurs premiers de tous les #nombres compris dans
#l'intervalle [n1,n2]
from math import sqrt #importation de la #fonction racine carrée
#------------------------------
n1,n2=2,1 #valeur pour rentrer dans l boucle
while (n1>n2): #Redemande la saisie des deux #nombres si (n1>n2)
n1=int(input("Entrer le pemier entier positif "))
n2=int(input("Entrer un second entier positif supérieur "))
print("Voici la décomposition en facteurs premiers des entiers entre ",n1," et ", n2)
#----------------------
T=[] #liste devenant tableau à deux dimensions #pour stockage des nombres et de leurs
# facteurs sans le 1
S=[] #tableau à deux dimensions pour stockage #des premiers nombres premiers
m=0
#--------------------
for i in range(0,n2-n1+1):
T.append([]) #crée le tableau à deux #dimensions vide
#---------------------
HH=range(3,int(sqrt(n2))+1)
c=0 #initialisation d'un compteur
S.append(2)
for i in HH: #Boucle pour la recherche des #nombres premiers plus petit que racine(n2)+1
m=int(sqrt(i))+1
c=2 #Commencer par le diviseur 1 n'est pas #utile
while (c<=m and i%c!=0): #Boucle tant qu'il n #y a pas de diviseurs (c est le diviseur)
c+=1
if (c>m): #Teste si le nombre est premier
S.append(i) #Stocke le nombre premier en #indice 0

#----------------------------------
HH=range(n1,n2+1)
for i in HH: #Boucle principale faisant varier #les valeurs dans l'intervalle [n1,n2}
T[i-n1].append(i) # valeur de l'entier stocké en #indice 0
c=0 #Initialisation du compteur
m=len(S)-1 #indice du dernier nombre premier #stocké dans le tableau S
nb=i #On stocke i dans nb pour pouvoir #modifier sa valeur (le diviser)
while(c<=m and nb>1): # On teste tous les #facteurs premiers et on s'arrete avant si on arrive #à 1
while (nb%S[c]==0): #Tant que S[c] est un #diviseur on divise nb par S[c]
nb=nb/S[c]
T[i-n1].append(S[c]) #on stocke le diviseur
c=c+1
if (nb!=1):
T[i-n1].append(nb) #Stocke la valeur i si i est #premier

#-------------------------------------
for i in range(0,n2-n1+1):
if len(T[i])==2:#Teste si le nombre est premier #(T[i][0]= 1 et T[i][1]=i )

print("------------------")
print("Le nombre ",T[i][0],"est premier") #T[i][0] est le nombre lui meme.
print("------------------")
else:
print("Liste des facteurs premiers de ",i+n1)
print(T[i][1:len(T[i])]) #Affiche tous les #facteurs premiers(l'indice 0 qui est l'entier n'est #pas affiché)

Programme4:
#Le programme demande d'entrer deux entiers n1 #et n2 (n2>n1) puis
#recherche les facteurs premiers de tous les #nombres compris dans
#l'intervalle [n1,n2]
from math import sqrt #importation de la #fonction racine carrée
#------------------------------
n1,n2=2,1
while (n1>n2): #Redemande la saisie des deux #nombres si (n1>n2)
n1=int(input("Entrer le pemier entier positif "))
n2=int(input("Entrer un second entier positif supérieur "))
print("Voici la décomposition en facteurs premiers des entiers entre ",n1," et ", n2)
#----------------------
T=[] #liste devenant tableau à deux dimensions #pour stockage des nombres et de leurs
# facteurs sans le 1
S=[] #tableau unidimensionnel pour stockage des #nombres premiers utiles
m=0
#--------------------
for i in range(0,n2-n1+1):
T.append([]) #crée le tableau à deux #dimensions vide
#---------------------
HH=range(3,int(sqrt(n2))+1)
c=0 #initialisation d'un compteur
S.append(2)
for i in HH: #Boucle pour la recherche des #nombres premiers plus petit que racine(n2)+1
m=int(sqrt(i))+1
c=2 #Commencer par le diviseur 1 n'est pas #utile
while (c<=m and i%c!=0): #Boucle tant qu il n #y a pas de diviseurs (c est le diviseur)
c+=1
if (c>m): #Teste si le nombre est premier
S.append(i) #Stocke le nombre premier

#----------------------------------
HH=range(n1,n2+1)
for i in HH: #Boucle principale faisant varier #les valeurs dans l'intervalle [n1,n2}
T[i-n1].append(i) # valeur de l'entier stocké en #indice 0
c=0 #Initialisation du compteur
m=len(S)-1 #indice du dernier nombre premier #stocké dans le tableau S
nb=i #On stocke i dans nb pour pouvoir #modifier sa valeur (le diviser)
while(c<=m and nb>1): # On teste tous les #facteurs premiers et on s'arrete avant si on arrive #à 1
while (nb%S[c]==0): #Tant que S[c] est un #diviseur on divise nb par S[c]
nb=nb/S[c]
T[i-n1].append(S[c]) #on stocke le diviseur
c=c+1
if (nb!=1):
T[i-n1].append(nb) #Stocke l'unique facteur #premier plus grand que racine(i)+1 ou la valeur i #si i est premier

#-------------------------------------
for i in range(0,n2-n1+1):
if len(T[i])==2:#Teste si le nombre est premier #(T[i][0]= 1 et T[i][1]=i )
print("------------------")
print("Le nombre ",T[i][0],"est premier") #T[i][0] est le nombre lui meme.
print("------------------")
else:
print("Liste des facteurs premiers de ",i+n1)
print(T[i][1:len(T[i])]) #Affiche tous les #facteurs premiers(l'indice 0 qui est l'entier n'est #pas affiché)

Programme5:
#Le programme demande d'entrer deux entiers n1 #et n2 (n2>n1) puis
#recherche les facteurs premiers de tous les #nombres compris dans
#l'intervalle [n1,n2]
from math import sqrt #importation de la #fonction racine carrée
#------------------------------
n1,n2=2,1
while (n1>n2): #Redemande la saisie des deux #nombres si (n1>n2)
n1=int(input("Entrer le pemier entier positif "))
n2=int(input("Entrer un second entier positif supérieur "))
print("Voici la décomposition en facteurs premiers des entiers entre ",n1," et ", n2)
#----------------------
T=[] #liste devenant tableau à deux dimensions #pour stockage des nombres et de leurs
# facteurs sans le 1
S=[] #tableau unidimensionnel pour stockage des # nombres premiers utiles
m=0
#--------------------
for i in range(0,n2-n1+1):
T.append([]) #crée le tableau à deux #dimensions vide
#---------------------
HH=range(3,int(sqrt(n2))+1)
c=0 #initialisation d'un compteur
S.append(2)
for i in HH: #Boucle pour la recherche des #nombres premiers plus petit que racine(n2)+1
m=int(sqrt(i))+1
c=2 #Commencer par le diviseur 1 n'est pas #utile
while (c<=m and i%c!=0): #Boucle tant qu il n #y a pas de diviseurs (c est le diviseur)
c+=1
if (c>m): #Teste si le nombre est premier
S.append(i) #Stocke le nombre premier

#----------------------------------
HH=range(n1,n2+1)
for i in HH: #Boucle principale faisant varier #les valeurs dans l'intervalle [n1,n2}
T[i-n1].append(i) # valeur de l'entier stocké en indice 0
c=0 #Initialisation du compteur
m=len(S)-1 #indice du dernier nombre premier #stocké dans le tableau S
nb=i #On stocke i dans nb pour pouvoir #modifier sa valeur (le diviser)
while(c<=m and nb>1): # On teste tous les #facteurs premiers et on s'arrete avant si on arrive #à 1
while (nb%S[c]==0): #Tant que S[c] est un #diviseur on divise nb par S[c]
nb=nb/S[c]
T[i-n1].append(S[c]) #on stocke le diviseur
c=c+1
if (nb!=1):
T[i-n1].append(nb) #Stocke l'unique facteur #plus grand que racine(i)+1 ou la valeur i si i est #premier

#-------------------------------------
for i in range(0,n2-n1+1):
if len(T[i])==2:#Teste si le nombre est premier #(T[i][0]= i et T[i][1]=i )
print("------------------")
print("Le nombre ",T[i][0],"est premier") #T[i][0] est le nombre lui meme.
print("------------------")
else:
print("Liste des facteurs premiers de ",i+n1)
print(T[i][1:len(T[i])]) #Affiche tous les #facteurs premiers(l'indice 0 qui est l'entier n'est #pas affiché)








Encore une fois Merci D'avance

[bolza]

Bonjour,

es-tu sûr des propositions de réponses pour la question 1 ?
car parmi les réponses possibles proposées, je n'en trouve aucune de correcte :/

[zozo42]

Bonjour,

J'ai eu le même probleme que vous, c'est donc pour cela que je n'arrive pas a la faire, donc le probleme ne vient pas de moi mais du sujet :S

[bolza]

Ce que tu peut faire c'est de dire (et de monter) que normalement le programme affiche ça
et que cela ne fait pas parti des solutions proposées. Ou alors le signaler à ton professeur.

[aymanemaysae]

Si on initialise X par a (un nombre entier naturel) et Y par b (un nombre entier naturel), donc :
1) Pour la première étape : X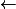 X + Y, la variable X contiendra a + b et Y contiendra b.
2) Pour la deuxième étape : Y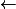 X - Y, la variable X contiendra a + b et Y contiendra (a +b) - b = a.
3) Pour la troisième étape : X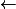 X - Y, la variable X contiendra (a + b) - a = b et Y contiendra a.
4) Pour la quatrième étape : X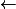 X + Y, la variable X contiendra a + b et Y contiendra a.
5) Pour la cinquième étape : Y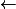 X + Y, la variable X contiendra a + b et Y contiendra (a + b) + a = 2 a + b.

[chan79]

Il doit y avoir une erreur de texte
On a la même chose après les étapes 2 et 4.

[zozo42]

Bonsoir,

Je l'ai signaler a mon professeur par Email j'attend donc ça réponse.
Avez vous des idée pour les questions suivantes ?

Merci d'avance.