Etude d'une fontion - fonctiona associés

[paul1234]

Bonjour, j'ai un exercice que je ne comprend pas, j'espere que quelqu'un puisse m'aider

énoncé:

L'objectif de cet exercice est d'étudier la fonction f définie sur R\{-1} par :

f(x)=(x^2+2x-3)/(x+1 )

[Manny06]

quelles sont les questions posées ?

[paul1234]

Bah enfaîte je dois étudier la fonction f, définie sur R\{-1} par : f(x)=(x^2+2x-3)/(x+1 ) ... et je ne sais pas comment faire

[laetidom]

Bah enfaîte je dois étudier la fonction f, définie sur R\{-1} par : f(x)=(x^2+2x-3)/(x+1 ) ... et je ne sais pas comment faire

Bonjour,

Je pense que la lecture (jusqu'au bout) du post de Mazigh du 01.03.16 à 16h16 peut beaucoup t'aider ! :

C'est toujours la même procédure (les grandes étapes) :

1) Domaine de Définition Df

2) Calcul dérivée :

3) Signe de f ' (x)

4) Tableau de variations sur Df

5) Tracé de l'allure de la courbe représentative de la fonction

[paul1234]

pouvez vous svp m'envoyez un lien du post de mazig ? je ne le trouve pas

et donc pour résoudre mon exercice je dois procéder par ces 5 étapes?

[laetidom]

pouvez vous svp m'envoyez un lien du post de mazig ? je ne le trouve pas

et donc pour résoudre mon exercice je dois procéder par ces 5 étapes?

lycee/derivee-tangente-t172397.html

[paul1234]

merci bcp

[laetidom]

merci bcp

Oui, 5 grandes étapes

Est-ce que tu y arrives ? . . .

[paul1234]

Non, je n'y arrive pas :s
J'ai chercher comment calculer le domaine de définition Df mais j'y arrive pas :s:s

[laetidom]

Non, je n'y arrive pas:s
J'ai cherché comment calculer le domaine de définition Df mais j'y arrive pas :s:s

Etape 1 :




le numérateur peut accepter tout x

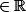
dénominateur : en maths, on ne peut pas diviser par 0 donc x+1 ne doit pas être nul donc x+1 <> 0
donc x doit être différent de - 1
le dénominateur étant plus restrictif que le numérateur, il l'emporte :

donc Df = - { - 1}

Comprends-tu ?

[laetidom]

Bonjour,

Etape 2 :

f(x) est de la forme

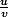
donc , non ? . . .


Soit ,

Peux-tu nous calculer f ' (x) . . . ?