Salut,
merci beaucoup pour ta contribution.
Oui, en effet, les rotations se font autours du même axe, mais selon un angle
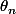
relatif à l'axe de l'angle "précédent" (disons

), et un centre de rotation à une certaine distance du précédent, dans la direction justement

.
L'origine géométrique de la construction n'est pas importante ici, mais juste la nature récursive de la définition des angles. La relation suivante est implicite si on utilise les relations type
)=x)
,
 = asin(\frac{x}{\sqrt{x^2+1}}))
, etc.. mais là voici comme demandé:
pour n>1 :
 = \frac{tan (\theta_{n-1})}{4})
pour n=1 :

cela implique :
pour n>1 :
 = \frac{tan \theta}{4^n})
Cette relation particulière et qui peut sembler arbitraire est le fruit d'une construction géométrique antérieure, mais dont l'unique contrainte se manifeste ici dans le rapport des longueurs des segments (1/2) et celui des
tangentes des angles (1/4)...
J'ajoute une image illustrant dans quel contexte surgit mon désespoir :
http://i.imgur.com/kHXSMow.pngici,
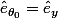
, et
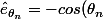\cdot\hat{e}_{\theta_{n-1}} + sin(\theta_n)\cdot\hat{e}_{\theta_{n-1}}^{\perp})
pour
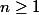
...
Tu as besoin que je définisse

aussi? Dis-moi si oui...
Il est donné par récurence aussi en imposant

sort part l'arrière du plan.
Et on arrive à cette matrice

en voulant exprimer

en fonction de

....
La multiplication des matrices sert justement à obtenir les coordonnées du point de convergence dans le plan (x,y)...
Le but ultime étant de calculer
 = R_x(\theta)\cdot \hat{e}_x + R_y(\theta)\cdot \hat{e}_y = \sum_{n=0}^{\infty} (\frac{1}{2^{n-1}})\hat{e}_{\theta_n})
!!
On sait déjà que le point de convergence pour
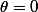
est le point (0, M) si on prend le point P0 du dessin comme origine. Où M = 2-1+1/2-1/4+1/8-1/16+.... = 1+1/3
Des idées pour m'aider à parvenir à trouver ce point?
Je ne suis pas un chercheur pro, j'ai fait des études en physique, et je m'intéresse en hobby, pour le moment, à ce problème...qui est parti de nulle part...
Pour ceux que ça intéresse, voici une autre illustration qui montre le contexte dans lequel est survenu le problème actuel :
http://i.imgur.com/k21s7Mx.pngLa contrainte sur les tangeantes des angles provient de la construction d'une séquence itérative de projections stéréographiques + homotéthie de rapport 1/2. Les courbes turquoises représentent les lieux des centres des arcs de cercles (oranges) issus de [POP1] (anciennement [FF']) et [P1P2] ([F'P'']) et qui se trouvent sur la médiatrice de [POP1] et [P1P2] respectivement, lorsque

varie de

à
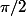
.
J'ai déjà obtenu une expression pour F(x) le lieu des points C' pour le domaine de theta. Can you guess it?
Ca ne sert pour le moment à rien...mais la courbe n'est pas triviale...et sa racine vaut

....
Mais évidemment, tout cela n'a jamais été vérifié, et si par l'occasion quelqu'un se sent l'âme de contribuer à cette aventure...qu'il n'hésite pas à vérifier mes calculs, car rien n'est sûr!
pour
de 1 à 7.
