Intégrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
razel
- Membre Naturel
- Messages: 54
- Enregistré le: 26 Juin 2015, 21:59
-
 par razel » 27 Fév 2016, 16:10
par razel » 27 Fév 2016, 16:10
Salut, j'ai un commencé cet exercice et je suis perdu :
Soit n appartenant à N on pose :


1 ) Calculer A(0) et B(0)
A(0) = 1
B(0) = 1
2) Montrer que :


J'ai essayé le raisonnement par récurrence vu qu'on nous demande de calculer les premiers termes.
Mais ça ne me donne pas grand chose.
Merci d'avance.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Fév 2016, 16:12
par Ben314 » 27 Fév 2016, 16:12
Salut,
Fait des intégration par parties si tu as vu ce que c'était.
Et sinon, applique la formule
dx=F(\frac{\pi}{2})-F(0))
à la fonction
)
puis à la fonction
)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
razel
- Membre Naturel
- Messages: 54
- Enregistré le: 26 Juin 2015, 21:59
-
 par razel » 27 Fév 2016, 16:54
par razel » 27 Fév 2016, 16:54
J'ai essayé avec l'intégration par parties mais ça fait deux pages de calcul.
Il faut intégrer deux fois puis faire la somme ; mais je pense qu'il doit y avoir une méthode plus facile.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 27 Fév 2016, 21:15
par Pisigma » 27 Fév 2016, 21:15
Bonsoir,
c'est effectivement plus court à calculer si tu considères que :
x}dx)
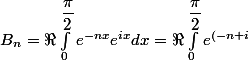x}dx)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Fév 2016, 10:29
par zygomatique » 28 Fév 2016, 10:29
salut
même sans IPP les indications de Ben314 invitent fortement à calculer ::
 = e^{-nx} \cos x)
donc
 = -(\sin x + n \cos x)e^{-nx})
et
 = e^{-nx} \sin x)
donc
 = (\cos x - n \sin x)e^{-nx})
il suffit alors de regarder pour voir ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités