Intégrale et applications

[razel]

Salut, je rencontre un petit problème au niveau de la compréhension du cours d'Intégrales et Primitives.

Voila : Quand on a abordé les applications de l'intégrales ; On a vu que si une fonction était continue et positive. L'intégrale de cette fonction entre a et b était égale à la surface délimitée par la courbe représentative de la fonction, l'axe des abscisses et les droites d'équation : x = a et x = b.
Ce que je ne comprends pas c'est le fait que l'intégrale qui est égale à F(b) - F(a) ; c'est)à-dire la primitive entre deux points distincs peut nous donner cette surface qui dépends de la fonction en chaque point situé entre a et b.

En formulant d'une autre manière : comment la les primitives de la fonction en deux valeurs a et b, peuvent nous renseigner sur cette surface ; qui dépend des images d'une infinité de valeurs entre a et b.

J'espère avoir bien formulé ma question

Merci d'avance pour vos lumières.

PS : on m'a donné l'exemple d'une fonction constante que j'ai compris, mais ça devient plus compliqué avec les autres fonctions.

[Ben314]

Salut,
Cela provient du fait que, lorsque tu as une primitive F d'une fonction f, cela signifie que, pour tout x de [a,b] on a F'(x)=f(x) donc au fond, ta primitive "contient" bien des information sur tout ce qui se passe entre a et b pour f et pas uniquement des informations concernant f(a) et f(b).

Par exemple, si une fonction f est définie sur [0,3], mais que tu ne la connais par exemple que sur [0,1] et sur [1,2], tu ne peut pas évaluer une primitive F sur [1,3], ni même calculer la valeur de F(3)-F(1).

[razel]

Merci beaucoup , c'est beaucoup plus clair maintenant. Existe-t-il une preuve compréhensible à mon niveau (terminale S)?

[Ben314]

Plus ou moins :
Tu prend une fonction positive continue f définie sur un intervalle [a,b] et qu'a tout réel c de [a,b] tu associe la "surface" (*) S(c) comprise entre l'axe des x, la courbe de f et les droites verticales x=a et x=b.
Comme f est continue (en c), si h est un réel suffisamment petit, f(c+h) reste "assez proche" de f(c) donc S(c+h) (qui est la surface sous la courbe entre les droites x=a et x=c+h) est a peu prés égal à S(c) plus la surface du rectangle de largeur h et de hauteur f(c) : donc et, en écrivant tout ça comme il faut, on montre en fait que ce qui montre qu'en fait S est la primitive de f qui s'annule en x=a (par définition même, on a S(a)=0).
Si F est une autre primitive de f, alors elle diffère de S d'une constante donc F(b)-F(a)=S(b)-S(a)=S(b) qui est la surface "sous la courbe" entre x=a et x=b.

(*) Le tout étant d'admettre qu'une telle "surface" existe.

[razel]

Merci beaucoup, c'est tout à fait clair maintenant.

[Pseuda]

Bonjour,

Dans l'expression F(b)-F(a), F(b) n'a pas de signification en soi pour la fonction f (car toute fonction F+k est une primitive de f), F(a) non plus. Ce qui compte, c'est F(b)-F(a). Les fonctions F(x) forment comme des lignes de niveaux, toutes parallèles entre elles, séparées par un écart k, et les F(b)-F(a) sont constants pour f.

Tu peux le voir par exemple, comme un compteur kilométrique d'une voiture allant de la ville A à la ville B. La distance parcourue au compteur entre A et B, est , avec 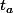heure de départ, 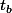heure d'arrivée, peu importe d'ailleurs les vitesses instantanées v(t) lors du trajet entre A et B.

F(t)=compteur kilométrique en fonction du temps t (après avoir choisi une origine t0, date de mise en service de la voiture)
v(t)=vitesse instantanée en fonction du temps t : F'(t)=v(t)