Calcul de valeurs propres
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sheik56
- Messages: 9
- Enregistré le: 21 Fév 2016, 16:18
-
par Sheik56 » 25 Fév 2016, 22:28
Bonjour,
je cherche à calculer les valeurs propres de la matrice suivante :
La consigne indique que les valeurs propres de cette matrice sont les racines de
=(X-(c_{2}P-r_{3}))(X^{2}+\alpha X+\beta ))
avec
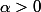
et
que l'on précisera.
)
me donne la matrice :
-X \end{Bmatrix})
J'ai tenté de développer par la 1ère ligne, j'en suis à l'expression suivante
^{i+j}\Delta=(-\frac{r_{1}}{K}N-X)(-X(-r_{3}+c_{2}P))+b_{1}N(b_{2}P(-r_{3}+c_{2}P)-X))
J'ai aussi essayé en suivant la 3ème ligne, mais sans succès, je ne parvient pas à retrouver la forme indiquée dans la consigne. Merci de votre aide
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
par Archytas » 26 Fév 2016, 00:25
Je pense que tu as fait deux erreurs de calcul, tu as dû t'embrouiller entre la première matrice A et A-XI en développant ou alors tu t'es embrouillé dans le parenthèsage parce que ça a pas l'air cohérent du tout ton polynôme.
Plus simplement, en observant la matrice A-XI quelques secondes est ce que tu peux pas déterminer à coup sûr une valeur propre ? Et cet indice là ne t'indique-t-il pas un choix plus judicieux de développement que par la première ligne ?
-
Sheik56
- Messages: 9
- Enregistré le: 21 Fév 2016, 16:18
-
par Sheik56 » 26 Fév 2016, 01:04
Je ne sais pas (ou pas encore) comment déterminer directement une valeur propre seulement en regardant la matrice, sauf si celle-ci est triangulaire ou diagonale. J'ai aussi tenté en développant par la 3ème ligne (car plus de 0) mais sans succès. Mais d'après la consigne, je comprend que
est une valeur propre.
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
par Archytas » 26 Fév 2016, 01:11
Le déterminant est nul si et seulement si la matrice est non inversible. En fait quand tu cherches les valeurs propres et que tu trouves par exemple a comme valeur propre alors A-a.I sera non inversible c'est à dire que tu auras une combinaison linéaire des colonnes nulle. De même pour les lignes. Donc si tu vois une valeur de X qui rend nulle toute une colonne ou toute une ligne c'est gagné, c'est une valeur propre ! Et donc on aura nécessairement (X- ...) dans notre polynôme. Et si tu essayais de développer par rapport à une
colonne bien choisie ? Techniquement tu dois arriver au même résultat quelle que soit la ligne ou colonne que tu choisisses mais certaines mènent plus facilement au résultat
-
Abuche
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Oct 2015, 20:17
-
par Abuche » 26 Fév 2016, 12:34
C'est un peu long et après calcul :
P(X) = - ( ..... ) ( ..... ) s'obtient avec un signe moins devant celui donné par l'énoncé
Valeurs propres :
-
Sheik56
- Messages: 9
- Enregistré le: 21 Fév 2016, 16:18
-
par Sheik56 » 26 Fév 2016, 15:16
Merci de vos réponse !
Voici mon calcul en développant par la 3ème colonne :
^{i+j}\Delta_{ij}} = c_{1}P((-\frac{r_{1}}{K}N-X*0)-(-b_{1}N*0))+((-r_{3}+c_{2}P)-X)(-X(-\frac{r_{1}}{K}N-X)+b_{1}b_{2}NP))
-X)(X^{2}+\frac{r_{1}}{K}N+b_{1}b_{2}NP))
A partir de là, vous dites que j'ai le droit de mettre un - devant la première parenthèse pour obtenir la forme
))
?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
par aymanemaysae » 26 Fév 2016, 16:15
Posons
donc
 = \begin{vmatrix} -u - X&-b_1&0\\b_2P&-X&-c_1P\\0&0&(- r_3 + c_2P) - X \end{vmatrix})
en développant suivant la
ligne on a :
 = ((- r_3 + c_2P) - X)\begin{vmatrix} -u - X&-b_1\\b_2P&-X \end{vmatrix})
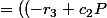 - X) (X^2 + uX+ b_1b_2P) = - (X - (- r_3 + c_2P)) (X^2 + uX+ b_1b_2P))
,
en posant
on a
 = - (X - (- r_3 + c_2P)) (X^2 + uX+ v))
et comme
 = - det(A-XI_3))
donc
 = (X - (c_2P - r_3)) (X^2 + uX+ v))
.
-
Sheik56
- Messages: 9
- Enregistré le: 21 Fév 2016, 16:18
-
par Sheik56 » 26 Fév 2016, 17:27
Merci pour toutes ces précisions =)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
