Problème polynômes, Applications linéaires, matrices

[Robot]

Ce que tu as fait ne va pas.
On te donne un système linéaire homogène de quatre équations à quatre inconnue. Sous forme matricielle,
.
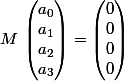
Connais-tu une condition nécessaire et suffisante sur pour que ce système ait une solution non triviale (dont les composantes ne sont pas toutes nulles) ?

[babeth107]

je ne vois pas, désolé ..

[Robot]

Tu n'as pas beaucoup réfléchi.
Voyons, les solutions du système forment le noyau de la matrice M.

[babeth107]

non je m'embrouille..
on prend un vecteur X = (a b c d) si x appartient Ker, AX= 0

[Robot]

Condition nécessaire et suffisante pour que le système ait une solution non triviale ?

[babeth107]

a,b,c ou d différent de 0 ?

[Robot]

Condition nécessaire et suffisante portant sur la matrice du système, bien sûr !
Bon, visiblement tu as l'air complètement à l'ouest sur le coup.
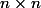
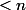
Soit une matrice . Alors le noyau de n'est pas réduit à si et seulement si le rang de est , si et seulement si n'est pas inversible, si et seulement si le déterminant de est nul.

[babeth107]

Ah Oui excusez-moi j'ai pas du tout suivi, j'ai du mal car c'est une partie que l'on a pas vraiment vu

Mais comment cette écriture m'indique-t-elles le résultat voulu ?

[Robot]

S'il te plait, essaie de récapituler ce qu'on a vu.

[babeth107]

D'accord, j'en suis a ce stade avec le système :
2* a2 + 3*a0 + a1(1-λ) = 0
3*a3 + 2* a1 + a2(1-λ) = 0
a2 + a3(1-λ) = 0
a1 + a0(1-λ) = 0

Je dois trouver les valeurs de λ

Or vous m'avez indiquer de procéder avec une matrice et un système linéaire et d'étudier le noyau de la matrice M
Or si il y a une solution non triviale M n'est pas inversible et le determinant de M non nul

[babeth107]

dois-je écrire la matrice M par rapport à mon système et voir pour quelle(s) valeurs de λ elle n'est pas inversible ?

[Robot]

Je dois trouver les valeurs de λ

Tu dois trouver les valeurs de telles que quoi ? Exprime toi précisément, l'effort de clarification que tu feras facilitera la communication et surtout te sera très utile pour comprendre.

Déjà la récapitulation te fait mieux voir où tu en es. Maintenant, agis !

[babeth107]

Je dois trouver les valeurs de λ pour remplir les conditions de ce système :
2* a2 + 3*a0 + a1(1-λ) = 0
3*a3 + 2* a1 + a2(1-λ) = 0
a2 + a3(1-λ) = 0
a1 + a0(1-λ) = 0

[babeth107]

Je trouve la matrice M=

La valeur de λ tels que la matrice est non inversible est donc 1?

[Robot]

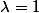
M est non inversible pour , mais ce n'est pas l'unique valeur telle que soit non inversible.
Ne connais-tu pas une condition nécessaire et suffisante pour qu'une matrice carrée soit non inversible ?

[babeth107]

le déterminant de la matrice est aussi nul

[Robot]

M est non inversible pour ,

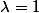
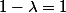
Dailleurs, non, ce n'est pas vrai. Pour , ce n'est pas inversible, mais aussi pour d'autres valeurs de .

[babeth107]

Ah oui ma matrice n'est même pas échelonnée je ne peux donc ma réponse était fausse.
Comment déduis-tu que ''Pour 1-λ=1 ce n'est pas inversible '' ? Une valeur de λ serait donc 0 ?
Pour trouver les autres valeurs de λ faut il que j’échelonne la matrice?
Je suis désolée j'ai vraiment du mal ..

[Robot]

Hum... Les déterminants, tu ne connais pas ?

[babeth107]

Nous avons vu la méthode du déterminant dans le cadre des matrices, pour inverser une matrice 2 colonnes, 2 lignes seulement.
Je sais qu'il faut utiliser le déterminant dans la question des valeurs propres de A j'ai regardé sur internet la méthode pour trouver le déterminant donc ça c'est bon mais j'avoue que je ne connais pas encore son utilisation