Matrices

[FunkyAnts]

Bonjour tout le monde,

j'ai un petit problème avec un exo sur les matrices :

En fait j'ai deux matrices 3*3

On me demande de déterminer une base dans laquelle la matrice A devient la matrice C.

Pouvez-vous me donner la méthode s'il vous plaît.

Ps: en fait j'ai essayé de trouver une matrice B=A^(-1)*C, mais ma matrice A n'est pas inversible !

Cordialement, merci pour votre aide.

[aymanemaysae]

En lisant cette merveille de Mme Annette Paugam sur le thème "Matrice de passage et changement de base", vous n'aurez dorénavant besoin - je l'espère - de l'aide de personne sur le sujet.

[FunkyAnts]

Merci aymanemaysae, mais ce cours est trop complexe pour mon niveau.

Il me perd davantage qu'il m'oriente.

Est-ce que je dois utiliser les valeurs propres de ma matrice A ? Et utiliser les vecteurs propres pour faire une matrice de passage ?


Cordialement.

[Robot]

Est-ce que la matrice C est diagonale ?

[FunkyAnts]

Elle est triangulaire supérieure.

[Robot]

Tu peux être plus précis, ou c'est confidentiel défense ?
Serait une mise sous forme de Jordan ?

[FunkyAnts]

Oui, je vais l'être.

Ma matrice A : A=

Je dois déterminer une base dans laquelle la matrice A devient la matrice C :


C=


En fait j'ai calculé les valeurs propres de A, qui valent L=0 et L=-5, donc le déterminant vaut 0.

[Robot]

Bon, c'est bien une mise sous forme de Jordan (sans le dire).
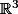Soit l'endomorphisme de de matrice dans la base canonique.
Si a la matrice dans une autre base 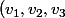, c'est que est valeur propre de multiplicité 2 de et que est valeur propre de multiplicité 1. Ca doit te permettre de déterminer et .
Ensuite, il suffit de lire la matrice pour voir ce qu'on demande à 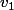, 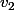et 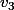. On demande :
(1)
(2)
(3)
(1) et (3) disent que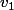 et 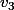sont des vecteurs propres de de valeurs propres associées respectivement et . Tu dois savoir trouver de tels vecteurs propres.
Il reste alors à trouver un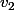 satisfaisant (2).

[FunkyAnts]

Merci Robot.