Suite d'intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Hoog
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Sep 2006, 00:02
-
 par Hoog » 01 Oct 2006, 19:17
par Hoog » 01 Oct 2006, 19:17
On considère l'intégrale
^n}{3} dx\)
avec n appartenant à

.
1. Montrer que la suite de terme général

est convergente.
2. En admettant que l'on a :
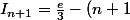I_n)
:
a. Calculer

b. Déterminer la valeur de l'intégrale
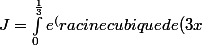) dx)
J'ai surtout des problèmes pour la question 1. et 2.b. (le reste ça va) - merci de m'aider ! :triste:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 01 Oct 2006, 19:27
par yos » 01 Oct 2006, 19:27
La suite est décroissante minorée (par 0) donc elle converge.
Pour le 2b, l'intégrale de la fonction réciproque est plus facile. D'où par symétrie...
-
Hoog
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Sep 2006, 00:02
-
 par Hoog » 02 Oct 2006, 10:06
par Hoog » 02 Oct 2006, 10:06
J'avais bien remarqué que exp(racine cubique de 3x) est la fonction réciproque de
^3}{3})
, c'est ok par ailleurs pour les bornes, mais est-ce que ça veut dire que
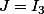
? Tu pourrais me détailler pourquoi exactement ?
Merci de ton aide, c'est sympa de ta part. :happy2:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 02 Oct 2006, 11:41
par tize » 02 Oct 2006, 11:41
Ca ne veut pas forcément dire que

, fais un dessin, le graphe de la fonction réciproque est obtenu par symétrie d'axe la droite d'equation y=x.
Si tu trouves l'aire situé en dessous du graphe de la fonction réciproque, avec un certain rectangle dont l'aire ne change pas tu en déduiras l'aire située en dessous de ta fonction à intégrer...
En espérant avoir été clair et...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités