Matrice diagonalisable ?

[FunkyAnts]

Bonsoir,

je sollicite votre aide pour une question d'un exo que je ne sais pas résoudre.

on a un système d'équations :
3x(t)-y(t)=
x(t)+y(t)=

J'en tire une matrice A=

Une valeur propre =2

Et un vecteur propre x=


En fait mon problème commence avec le fait que l'on me demande des valeurs propres et des vecteurs propres, alors que je n'en trouve qu'une et qu'un !

Ensuite on demande si la matrice A est diagonalisable ?
Je pensais le faire avec la formule P^(-1)AP, mais comme je n'ai qu'un vecteur propre je ne peux pas avoir de matrice de passage ? Si ?


Cordialement.

[zygomatique]

salut

essayer de résoudre l'équation Au = 2u avec u = (a, b) ... pour trouver un éventuel autre vecteur propre ....

sinon la matrice n'est pas diagonalisable ....

[Ben314]

Je sais pas si c'est vraiment la peine d'essayer : si le s.e.v. associé à la v.p. 2 était de dimension 2, ça voudrait dire que A=...

Enfin, bref, ta matrice A n'est pas diagonalisable et... il faudra faire avec pour la suite de l'exercice....

[jlb]

salut considère (1,0) et la matrice de passage P=

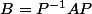
calcule alors , tu résous alors Y'=PY et tu obtiens ( sauf erreur) X = PY comme solution de ton système initial.

[FunkyAnts]

Merci pour vos réponses,

Néanmoins jlb, tu me dis qu'il y a une matrice de passage sans que ma matrice A soit diagonalisable ? Est-ce cela ?

[jlb]

oui, vous pourrez ainsi trigonaliser la matrice et le système sera très simple à résoudre