Problème que je comprend pas

par **Captain America** » 30 Sep 2006, 12:13

Salut salut,
Voilà, j'ai un problème là que je comprend pas, je vous le mets:

J'ai une parabole P d'équation y=x²-3x+1
On me dit que A et B sont les points de P d'abscisses respectives a et b avec a différent de b.
Il faut que je démontre que le coefficient directeur de la droite (AB) est a+b-3.

Comment que je fais????

Merci.

par **tize** » 30 Sep 2006, 12:28

Il suffit de calculer

: le coefficient directeur de la droite (AB)

par **Captain America** » 30 Sep 2006, 18:39

Ben le problème c'est que je les connait pas les coordonnées des points B et A. Sinon ça serait trop facile.

par **anima** » 30 Sep 2006, 18:44

tize a écrit:Il suffit de calculer : le coefficient directeur de la droite (AB)

Tu remplace x par a et b, tu simplifies, et ensuite tu trouve l'inclinaison de la corde sur cette parabole (AB quoi). Je le ferai ainsi, perso.

par **Captain America** » 30 Sep 2006, 20:08

Oulaahhh, j'ai pas trop compris là. Je répéte que je connais pas les coordonnées de A et B et que le problème est le suivant:

J'ai une parabole P d'équation y=x²-3x+1
On me dit que A et B sont les points de P d'abscisses respectives a et b avec a différent de b.
Il faut que je démontre que le coefficient directeur de la droite (AB) est a+b-3.

Voilà, si quelqu'un peut mer éexpliquer avec des exemples en cas ça serait cool.

Merci.

par **Imod** » 30 Sep 2006, 22:23

Je vais essayer d'expliquer autrement ( que mes prédécesseurs m'excuse car je les avais trouvés très clairs ) . Le coefficient directeur de la droite passant par les deux points A(xA,YA) et B(xB,YB) est donné par d = (yB-yA)/(xB-yB) .
Si on considère deux points de P alors yA et yB sont donnés par les formules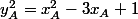

et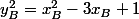

et alors après une petite factorisation et une petite simplification : d =a+b-3 .

Imod

par **Captain America** » 01 Oct 2006, 09:28

Ok je comprends maintenant. Merci beaucoup. En fait je pouvais pas comprendre je connaissais pas les formules.

Merci encore.

par **Captain America** » 01 Oct 2006, 10:04

Euh, par contre I-mod, t'es sur de ta formule d = (yB-yA)/(xB-yB) ????
Au niveau de (xB-yB).

par **Captain America** » 01 Oct 2006, 10:33

Bon en fait j'ai essayé et j'y arrive toujours pas. J'ai fait:
d=(yB-Ya)/(xB-Xa)
d=[(xB²-3xB+1)-(xA²-3xA+1)]/xB-xA
d=(xB²-3xB-xA²+3xA)/xB-xA
d=[xB(x-3)-xA(x-3)]/xB-xA
d=[(x-3)(xB-xA)]/xB-xA

Et après je suis bloqué.

par **Captain America** » 01 Oct 2006, 12:37

Nobody?? :cry:

par **Captain America** » 01 Oct 2006, 19:49

Vraiment personne???

par **Alpha** » 01 Oct 2006, 19:54

Salut, Imod s'est trompé, il faut remplacer le (xB - yB) par (xB-xA) dans la formule donnant d.
Sinon tout ce qu'il a dit est valable et tu as normalement tout ce qu'il faut pour finir.

par **Alpha** » 01 Oct 2006, 19:56

Euh et pourquoi ne simplifies-tu pas par (xB - xA) dans ta dernière équation? Il apparaît au numérateur et au dénominateur...

par **allomomo** » 01 Oct 2006, 19:58

Salut,

Je calcule la pente de la droite (AB)
On considère les points :
A(a, P(a))
B(b, P(b))

Donc

par **Alpha** » 01 Oct 2006, 20:00

Captain America a écrit:d=(xB²-3xB-xA²+3xA)/xB-xA
d=[xB(x-3)-xA(x-3)]/xB-xA

C'est une blague? Le A et le B ce sont des indices, pourquoi lorsque tu factorises par xB, obtiens-tu xB(x-3) ??

Ce que tu dois écrire, c'est que xB²-3xB = xB(xB-3). Du coup la simplification que j'ai mentionné précédemment n'est plus possible.

Problème que je comprend pas

Problème que je comprend pas

Qui est en ligne