Complexes

[razel]

Bonsoir à tous ;
Je voudrais savoir comment, en ayant la valeur de deux complexes z et z' affixes respectifs des points M et M',
montrer que le triangle OMM' est isocèle en O.
J'ai entendu dire qu'après avoir démontré qu'il est isocèle il faut montrer qu'il n'est ni équilatéral ni isocèle rectangle. Pouvez-vous me renseigner sur cela aussi.
Merci d'avance.

[Carpate]

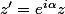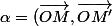Si z et z' sont liés par la relation , avec , alors le triangle OMM' est isocèle en O.
Cela n'exclut pas le fait que ce triangle peut être aussi rectangle en O ou équilatéral ...
Mais tu ne donnes pas les valeurs de z et z' (secret défense ?)

[Ben314]

Salut,
Perso, je serait parti sur le fait que OMM' est isocèle en O ssi OM=OM' or OM=... et OM'=...

[razel]

Merci d'avoir répondu

Voici les valeur de z1 et z2 :

z1 =
z2 =

avec -90°<a<90°

Désolé de ne pas avoir donné les angles en radian, j'ai quelques problèmes avec le latex

En fait la question est de déterminer la nature du triangle OMM'

[Carpate]

.........
Ensuite, selon les valeurs de a, le triangle OMM' pourra être rectangle isocèle, équilatéral

[Ben314]

Mon petit doigt me suggère qu'il va quand même être "assez souvent" isocèle en O...

[Carpate]

Je suis sûr que Razel aura conclu ce que mes ...... suggéraient et que ton "petit doigt t'a suggéré"

.........

La suite de ma réponse répondait à la formulation de :

J"'ai entendu dire qu'après avoir démontré qu'il est isocèle il faut montrer qu'il n'est ni équilatéral ni isocèle rectangle. Pouvez-vous me renseigner sur cela aussi"

J'ose espérer que ce ne sont pas les termes de l'énoncé. Rien n'interdit à a les valeurs :