Petit exercice de topologie

[ArtyB]

Bonjour,

Petit exercice de topologie, qui je suppose doit se faire en combinant l'utilisation de plein de petites propriétés de cours, mais c'est quelque chose que j'ai beaucoup de mal à faire ça.

On munit , n>=2 d'une norme quelconque ||.||
1. Soit . L'application de dans qui à x associe est elle continue sur ? Justifier.
2. La sphère unité est elle ouverte ? fermée ? Bornée ?
3. En déduire que la quantité est bien définie et montrer qu'il existe tel que
4. Montrer , on utilisera la linéarité de T.
5.En déduire puis qu'en fait c'est une égalité.
6. La boule fermée unité est elle fermée ? bornée ? Déterminer son bord.
7. Montrer que.

1. Je dirais que T étant une application linéaire, elle est continue ssi est de dimension finie. Et si T est continue alors sa norme l'est aussi ?

[Ben314]

Salut,
Déjà, il y a une grosse boulette dans l'énoncé, vu que x->||T(x)||, c'est surement pas une application de dans .

Ensuite, il y a un truc qui me semble pas super clair : pour parler de continuité d'une fonction de dans , il faut évidement avoir une topologie sur les deux espaces.
Sur , pas de soucis, c'est la "topologie usuelle" qu'on prend, mais sur , c'est pas super clair vu qu'on peut soit prendre la "topologie usuelle", soit celle induite par la norme ||.|| donné par l'énoncé.
Évidement, si on sait que toutes les normes sont équivalentes sur , alors ça ne change rien , mais vu le coté basique de l'exercice, je me demande si on est sensé ou pas utiliser ce résultat.

A froid, j'aurais tendance a dire qu'on considère qu'on sait que toutes les normes sont équivalentes sur (résultat tout sauf trivial) vu que, vu sous cet angle, il n'y a plus d'ambiguïté d'énoncé.

[ArtyB]

Merci de ta réponse Ben314,

En quoi est-ce que ça n'est pas possible ?
J'ai lu quelque part que toutes les normes sont équivalentes sur mais je ne sais pas ce que cela implique ? (je n'ai sans doute pas très bien compris la notion d'équivalence de norme mais je n'ai pas réussis à trouver de définition/explication claire).

[zygomatique]

salut

alors tu as mal travaillé ...

il suffit de taper "normes équivalentes" dans un moteur de recherche pour avoir la réponse ...

[alm]

Bonjour

pour parler de continuité d'une fonction de dans , il faut évidement avoir une topologie sur les deux espaces.

Je crois que l'énoncé fixe une norme dès le départ sur notée et que désormais c'est la topologie associée à cette norme qu'il considère.

[alm]

Merci de ta réponse Ben314,
En quoi est-ce que ça n'est pas possible ?

Ben314 veut dire que si alors .
L'énoncé devrait donc parler de comme application de vers .
Essaye donc de prouver que l'application: est continue.
Indication : lipschitzienne ?

[Ben314]

Je crois que l'énoncé fixe une norme dès le départ sur notée et que désormais c'est la topologie associée à cette norme qu'il considère.

Je continue à hésiter vu que, si on considère uniquement que la topologie est induite par la norme donnée (sans savoir qu'elle est équivalente aux normes usuelles), il me semble qu'on va être "coquin" à la question 3) où il faudra utiliser le fait que la sphère unité pour cette norme est compacte (pour la topologie issue de la norme en question).
Non ?

[zygomatique]

la dimension finie ne suffit-elle pas à lever ton hésitation ? .... (même sans savoir que les normes sont équivalentes)

[Ben314]

Oui... et non...
Lorsque tu écrit que les compacts de R^n sont très exactement les fermés bornés de R^n,
- Soit tu as montré AVANT que toutes les normes sont équivalentes et il n'y a aucune ambiguïté sur le sens des termes "compact", "fermé" et surtout "borné".
- Soit tu l'as pas encore démontré et il faut bien sûr préciser ce que tu entend par "compact", "fermé" et surtout "borné" (i.e. borné pour quelle norme ?)
Et si tu démontre que le résultat en question est en fait valable pour n'importe quelle norme, alors, tu viens du même coup de démontrer qu'elle sont toutes équivalents (vu que tu as montré que le terme de "borné" désignait la même chose quelque soit la norme envisagée sur l'espace...)

Bref, j'ai bien l'impression qu'il faut supposer tout ces résultat comme "connus" pour attaquer l'exercice (ce qui le rend terriblement trivial...)

[zygomatique]

ok effectivement ... mais je ne comprends pas trop ...


soit n une norme de l'espace vectoriel V = R^n et E une partie de V

n'as-t-on pas les définitions :

E est borné :: s'il existe M > 0 tel que pour tout x de E : n(x) < M alors E est borné

E est fermé :: si pour toute suite (x_n) de E convergeant vers x (<=> n(x_n - x) --> 0)alors x appartient à E alors E est fermé

E est compact : si E est fermé et borné alors E est compact

ou ces définitions ne conviennent-elles pas ? (de plus la dimension de V n'intervient même pas dans ces définitions)

merci par avance ....

[alm]

[réponse provisoire en attendant celle de Ben314]
Ce qui se fait:
On donne d'abord la définition de partie compacte de muni de la norme
Une partie est compacte si de toute suite d'éléments de on peut extraire une sous-suite convergente vers un élément de .

Avec cette définition:
Tout compact de est fermé borné : facile
Réciproque : Toute partie fermée bornée de est compacte: non facile à démontrer et ça necessite justement de prouver au préalable que dans , toutes les normes sont équivalentes

[Ben314]

ok effectivement ... mais je ne comprends pas trop ...
soit n une norme de l'espace vectoriel V = R^n et E une partie de V
n'as-t-on pas les définitions :
(1) E est borné :: s'il existe M > 0 tel que pour tout x de E : n(x) < M alors E est borné
(2) E est fermé :: si pour toute suite (x_n) de E convergeant vers x (<=> n(x_n - x) --> 0)alors x appartient à E alors E est fermé
(3) E est compact : si E est fermé et borné alors E est compact
ou ces définitions ne conviennent-elles pas ? (de plus la dimension de V n'intervient même pas dans ces définitions)
merci par avance ....

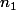
Je suis tout a fait d'accord avec alm : (1) et (2) sont des définitions qui, justement, montrent qu'a priori (i.e. sans savoir que toutes les normes sont équivalentes sur un e.v. de dim. finie) la notion de "fermé" et de "borné" sont relative à une norme donnée : une partie fixée pourrait très bien être bornée (et/ou fermée) pour une certaine norme et non bornée (et/ou non fermée) pour une autre norme . 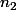C'est d'ailleurs fréquemment le cas en dimension infini où les normes ne sont pas toutes équivalentes.
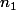
Ensuite, le (3), ce n'est pas du tout une définition, mais un théorème : la définition d'un compact, c'est souvent celle donné par alm (*) qui est valable dans tout espace métrique et qui, de nouveau, dépend de la norme choisie vu qu'à priori, une suite peut être convergente pour une certaine norme et non convergente pour une autre norme .
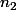
Et le problème, c'est que dans ce théorème, si on ne sait pas au préalable que toutes les normes sur R^n sont équivalentes, il faut préciser ce qu'on entend par "compact", "fermé" et "borné", c'est à dire préciser la norme utilisée pour la définitions de ces termes.

(*) Assez fréquemment on voit plus tard la définition avec des recouvrement d'ouverts adaptée au cas de la topologie générale, mais ça dépend des profs/bouquins.

[zygomatique]

ok merci beaucoup à vous deux ....

effectivement (3) n'est pas une définition mais un théorème .... oui j'avais oublié sa "vraie" définition ....

oui en fait je vois mieux le pb qui se pose ....

merci encore ...

[ArtyB]

1) Toutes les normes étant équivalentes sur , s'il l'une est continue, alors elle le sont toutes.
2) Une sphère peut être définie comme une boule fermée de centre x et de rayon r tq N(y-x)<=r où N est une norme quelconque et ici en prenant y=0 on se situe bien dans le cas d'une sphère. Donc elle est fermée.
Et pour tout x de on a ||x||=1 donc il existe une boule fermée B(0,1) telle que la sphère soit contenue dans cette boule, donc la sphère est bornée.
3) La sphère étant bornée et fermée, c'est un compact de .
Comme la sphère est compacte et que T est continue, alors T atteint son maximum sur la sphère. Donc la quantité ||T|| est bien définie et il existe de la sphère tel que||T(a)||=||T||.
4)Pour tout y de , on a ||T(y+0)||=||T(y)||=||T(y)||-||T-0)||<=M||y|| pour M une constante
et on peut prendre M=||T||.
5) D'après la question précédente, T est||T||-lipschitzienne et donc ||T|| est la plus petite constante C telle que ||T(y)||<=C||x|| et ainsi on a

6) Come l'inégalité définissant les x appartenant à B n'est pas stricte, alors B est fermée.
et donc B est bornée.
son bord est c'est donc la sphère.
7)D'après la question 3, et on a aussi B connexe et T continue.
Donc T atteint son maximum sur B et

[zygomatique]

il est dommage pour la 4/ de ne pas se servir de 3/

soit y dans R^n non nul et x = y/||y||

alors ||x|| = 1 donc x appartient à la sphère unité

donc T(y) = T(||y||x) = ||y||T(x) (linéarité de T) ....

en passant à la norme et en utilisant 3/ :: ||T(y)|| =< ||y|| ||T(a)|| <=> ||T(y)|| =< ||y|| ||T||

5/ on se fout un peu que T soit lipchitzienne ....

se déduit de 4/ en passant au sup et pas continuité seulement

[ArtyB]

4. Malin oui je n'y avais pas pensé, j'ai du mal à me reservir des questions précédentes
5. Comment ça ? Comment est-ce qu'on peut passer au sup par continuité seulement ?

[zygomatique]

ben si ||T(y)||/||y|| est majoré par ||T|| pour tout y non nul il semble bien que ce soit le cas du sup .... par définition du sup (plus petit des majorants)