Salut,
J'ai besoin d'aide concernant cet exercice :
1 )Calculer A = 1+cosx + cos 2x + ...... + cosnx
2)Calculer la limite de :
Un = 1/n ((sin(π/n) + sin(2π/n) + ..... + sin((n-1)π/n))
J'ai essayé d'utiliser la forme exponentielle mais après développement ça n'a rien donné.
Merci d'avance.
Complexes, Suites
6 messages
- Page 1 sur 1
Re: Complexes, Suites
Salut,
Pour le 1), il faut effectivement passer par la "forme exponentielle", et éventuellement constater que cos(x), c'est la partie réelle de exp(i.x).
Ensuite, il faut aussi utiliser les suites géométrique, et plus précisément la valeur de lorsque q est un complexe différent de 1.
lorsque q est un complexe différent de 1.
Pour le moment, tu as écrit que A était égal à quoi ?
Pour le 1), il faut effectivement passer par la "forme exponentielle", et éventuellement constater que cos(x), c'est la partie réelle de exp(i.x).
Ensuite, il faut aussi utiliser les suites géométrique, et plus précisément la valeur de
Pour le moment, tu as écrit que A était égal à quoi ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Complexes, Suites
Oui, ça m'a l'air bon. Avec du MimeTeX (met toi y...) ça donne
x}}{1-e^{ix}}+\dfrac{1-e^{-i(n+1)x}}{1-e^{-ix}}\Big))
Attention à bien préciser que cette formule n'est valable que si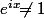 (sinon "division by zéro error"...)
(sinon "division by zéro error"...)
Ensuite, si on est courageux, on peut essayer d'écrire ça un peu différemment, histoire par exemple d'un peu mieux voir que le nombre en question est un réel.
Il y a plusieurs méthodes, et comme j'ai un peu la flemme de rentrer dans les subtilités, là, je t'inciterais juste à réduire au même dénominateur (les autres méthodes sont un peu plus courtes...).
Ton dénominateur "commun" étant de la forme avec
avec 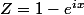 , c'est un réel et en ce qui concerne le numérateur, si tu développe tout puis que tu revient avec des notations en sinus et cosinus, les imaginaires purs vont disparaitre.
, c'est un réel et en ce qui concerne le numérateur, si tu développe tout puis que tu revient avec des notations en sinus et cosinus, les imaginaires purs vont disparaitre.
Sinon, un truc plus astucieux, c'est de voir que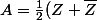=\text{R\'e}(Z)) où
où x}}{1-e^{ix}})
Ensuite, que ce soit le numérateur où le dénominateur, ils sont de la forme et une astuce classique consiste à écrire que
et une astuce classique consiste à écrire que 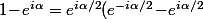=e^{i\alpha/2}\times -2i\sin(\alpha/2))
Attention à bien préciser que cette formule n'est valable que si
Ensuite, si on est courageux, on peut essayer d'écrire ça un peu différemment, histoire par exemple d'un peu mieux voir que le nombre en question est un réel.
Il y a plusieurs méthodes, et comme j'ai un peu la flemme de rentrer dans les subtilités, là, je t'inciterais juste à réduire au même dénominateur (les autres méthodes sont un peu plus courtes...).
Ton dénominateur "commun" étant de la forme
Sinon, un truc plus astucieux, c'est de voir que
Ensuite, que ce soit le numérateur où le dénominateur, ils sont de la forme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
