Domaine de définition de fonction à 2 variables

[angel_sm]

bonjour ,
j'ai besoin de votre aide sur une question
donnez le domaine de définition + le graph de la fonction suivante :
f(x,y)=ysin(1/ ((y²-x²)^1/2))
cela veut dire y²-x²>0 (y-x)(y+x)>0 et j'arrive pas a dessiner le graph
merci d'avance

[aymanemaysae]

Bonjour,

tout d'abord il faut traduire (y - x)(y + x) > 0, c-à-d un produit a * b est strictement positif quand:

((a est ....) et (b est ....) ou (a est ....) et (b est ....)) .

Dîtes-moi pour cet exercice ce que ça donne, ensuite on continuera.

[aymanemaysae]

Pour le graphe de cette fonction, je suis sûr qu'on vous a demandé de donner son graphe et non de le représenter, le tracer ou le dessiner , ce qui donnera une surface dans , ce qui n'est à la portée de personne .

[angel_sm]

c'est positive lorsque (y - x)>0 et (y + x)>0 ou (y - x)<0 et (y + x)<0 , il nous a demandé de tracer le graph ça sera en 3D)

[aymanemaysae]

Bien vu, donc on a ou

ou



Si vous arrivez à remplir les pointillés vous aurez trouvé le domaine de définition.

J'attends votre réponse et continuera.

[Ben314]

Salut,
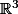Juste une question : tu es vraiment sûr qu'on t'a demandé de représenter le graphe de la fonction (qui est une partie de ) et pas uniquement de représenter l'ensemble de définition de (qui lui est une partie de ) ?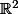

C'est évidement possible, mais c'est un peu inhabituel comme question (ou alors en précisant "en utilisant tel ou tel logiciel" vu que à la main, d'arriver à faire une perspective à peu prés potable...)

[angel_sm]

aa oui je suis désolée c'était un erreur j'ai mal exprimé .. c'est comme vous avez dit représentation de l'ensemble ,
alors c'est y>-x ou y<x
si c'est juste pour la représentation on doit tracer la droite -x et x ??

[aymanemaysae]

Bien vu, donc on a ou

ou



Si vous arrivez à remplir les pointillés vous aurez trouvé le domaine de définition.

J'attends votre réponse et continuera.

puisque vous avez ça veut dire que y > |x| et comme vous avez çà veut dire que y < - |x|, donc en traçant les courbes des fonctions g et h telles que et vous pouvez délimiter sur le tracé le domaine de définition de f .

[angel_sm]

c'est ce que j'ai fais merciii beaucoup ^^