Sous-espace vectoriel et base

[FunkyAnts]

Bonjour,

je sollicite votre aide pour une question dans un exo :

On considère l'ensemble des triplets de réels (x,y,z) qui vérifient 2x-y-z=0. Montrer qu'il s'agit d'un sous-espace vectoriel de R^3 et en donner une base.


Alors j'ai besoin de votre aide car en fait je n'arrive pas à le montrer ni à trouver une base.

[Robot]

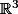
Commençons par le début : comment vérifier qu'un sous-ensemble d'un espace vectoriel (ici ) est un sous-espace vectoriel ?
La réponse est dans ton cours.

[FunkyAnts]

Il est simplement dit que les solutions d'une équation homogène de ce type forment un sev de R^n de dimension n-1.

Donc ici c'est un hyperplan de dimension deux.

Mais je n'arrive pas à trouver même avec mon cours comment le montrer.

[Ben314]

Salut,
Si je comprend bien, vous avez vu en cours des propriétés qu'on les sous-espaces vectoriels, mais on ne vous a jamais donné la définition de ce qu'est un sous espace vectoriel ?

[Robot]

Attends, tu me dis que tu as un cours qui parle de sous-espace vectoriel sans définir ce qu'est un sous-espace vectoriel ?
J'ai un peu de mal à y croire.

[FunkyAnts]

C'est un cours par correspondance. C'est franchement pas clair. De plus ils utilisent dans le cours des pré-requis que je n'ai pas, et je ne dois pas être le seul !

[Robot]

Il n'y a pas dans ton cours de définition de ce qu'est un sous-espace vectoriel ?
Un sous-ensemble F d'un espace vectoriel est un sous espace vectoriel si et seulement si
1) 0 appartient à F
2) F est stable par somme : la somme de deux éléments de F est toujours dans F
3) F est stable par multiplication par un scalaire : le produit d'un élément de F par n'importe quel scalaire est toujours dans F.