Limite d'une suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
makak06
- Membre Naturel
- Messages: 38
- Enregistré le: 24 Oct 2005, 22:53
-
 par makak06 » 30 Sep 2006, 20:30
par makak06 » 30 Sep 2006, 20:30
Salut a tous,
Voila j'ai un exo a faire et j'aimerais savoir si j'ai fais juste ou pas merci a vous !!
Soit f la fonction f definie sur [1 ; +[ par f(x) = racine (x^3-1)
Etudier la dérivabité de f en 1
Voici ce que j'ai fais :
j'utilise la formule : f(x) - f(a) / x - a
= racine (x^3-1) - 0 / x - 1
= racine (x^3-1) / x - 1
on sais que lim de racine (x3-1) tend vers 0 (quand x -> 1)
La limite de x-1 quand x-> 1 est egal a 0 mais sa me donne donc lim de 0/0 et je crois que c'est une limite indeterminé ou du moin je dois pouvoir simplifier plus haut mais comment svp ? :doh:
Merci d'avance :happy2:
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 30 Sep 2006, 20:36
par theluckyluke » 30 Sep 2006, 20:36
makak06 a écrit:
on sais que lim de racine (x3-1) tend vers 0 (quand x -> 1)
euh... je comprend pas ça...

en fait ce serait carrément
 = \sqrt{2})
non?
-
makak06
- Membre Naturel
- Messages: 38
- Enregistré le: 24 Oct 2005, 22:53
-
 par makak06 » 30 Sep 2006, 20:38
par makak06 » 30 Sep 2006, 20:38
Non desolé j'avais oublié de preciser que c'était une puissance, mais sayé c'est edité,
PS : Quand vous utiliser la fonction TEX comment connaissez vous les racourcie ?
-
makak06
- Membre Naturel
- Messages: 38
- Enregistré le: 24 Oct 2005, 22:53
-
 par makak06 » 30 Sep 2006, 20:42
par makak06 » 30 Sep 2006, 20:42
Oui je suis d'accord mais je dois pas plus expliqué le detail ? on ne peut pas simplifié avant de dire que c'est egal a 0...
La est ma question :marteau:
Merci pour le lien :happy2:
-
makak06
- Membre Naturel
- Messages: 38
- Enregistré le: 24 Oct 2005, 22:53
-
 par makak06 » 30 Sep 2006, 20:45
par makak06 » 30 Sep 2006, 20:45
theluckyluke a écrit:en gros c'est ça alors?
 = \sqrt{x^3+1})
définie sur

Oui mais avec un - donc
 = \sqrt{x^3-1})
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 30 Sep 2006, 20:51
par theluckyluke » 30 Sep 2006, 20:51
makak06 a écrit:Oui mais avec un - donc
 = \sqrt{x^3-1})
makak06 a écrit:La limite de x-1 quand x-> 1 est egal a 0 mais sa me donne donc lim de 0/0 et je crois que c'est une limite indeterminé ou du moin je dois pouvoir simplifier plus haut mais comment svp ?
non la limite en 1 est de
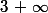
regarde la courbe de la fonction
essaye de t'orienter vers là :
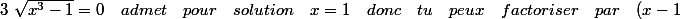)
 = (x-1)(x^2+x+1))
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 30 Sep 2006, 21:11
par theluckyluke » 30 Sep 2006, 21:11
 = (x-1)(x^2+x+1))
donc
} = \sqrt{(x-1)(x^2+x+1)})
donc
(x^2+x+1)}}{x-1})
=
(x^2+x+1)} \times \sqrt{(x-1)(x^2+x+1)}}{(x-1) \times \sqrt{(x-1)(x^2+x+1)}})
=
}{\sqrt{(x-1)(x^2+x+1)}} = + \infty)
car
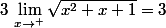
et
(x^2+x+1)} = 0^+)
je pense que c'est ça?
qu'est-ce que t'en dit?
-
makak06
- Membre Naturel
- Messages: 38
- Enregistré le: 24 Oct 2005, 22:53
-
 par makak06 » 30 Sep 2006, 22:11
par makak06 » 30 Sep 2006, 22:11
Ben tout ceci ma l'air juste mais comment peut on le verifier ?
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 01 Oct 2006, 10:47
par theluckyluke » 01 Oct 2006, 10:47
makak06 a écrit:Ben tout ceci ma l'air juste mais comment peut on le verifier ?
demander à quequ'un d'autre ou prendre ta calculatrice et tracer la fonction. Vas ensuite dans Table puis définis un intervalle petit (comme 0.01) et commence ta table à 1, tu verras que pour

ta fonction tend vers
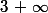
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
