ona n>=1:
en deduire l'expression de
Suite integral
6 messages
- Page 1 sur 1
suite integral
par ayabaklouti » 17 Jan 2016, 12:20
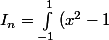soit }^n} ; n\succ 0)
evec n est un entier naturelle
ona n>=1:
*I_{n}=-2*n*I_n)
en deduire l'expression de
en fonction de n
ona n>=1:
en deduire l'expression de
Re: suite integral
par Ericovitchi » 17 Jan 2016, 13:15
heu non, l'intégration par partie a dû te donner plutôt : I_n= -2nI_{n-1})
écris ces équations pour n = 1;2;.... les unes en dessous des autres. Multiplie les membre à membre et tu trouveras In en fonction de n.
écris ces équations pour n = 1;2;.... les unes en dessous des autres. Multiplie les membre à membre et tu trouveras In en fonction de n.
Re: suite integral
par ayabaklouti » 17 Jan 2016, 14:05
Oui c vrai j ai fait une faute d ecriture c est I_{n-1} a la fin merci bien mais pour la deduction j ai suit la methode que tu m 'indique et je ne peut pas trouve la resulta si vous plais donner mois comment je peut avoir une solution en detail
Re: suite integral
par Ericovitchi » 17 Jan 2016, 16:53
tu écris la formule pour n = 1;2;...;n
I_n = -2nI_{n-1})
I_{n-1} = -2(n-1)I_{n-2})
----------------------------------
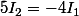
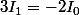
(et on connait 
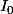
= 2)
______________________________ tu multiplies toutes ces égalités membre à membre
)I_n = (-2)(-4)...(-2n) * 2)
les autres I se simplifient
Après tu peux essayer de simplifier des trucs parce que(-4)...(-2n) = (-1)^n 2^n n!)
et = (2n+1)!/(2^n n!))
donc on peut écrire le résultat :
^n 2^{2n+1} n!^2}{(2n+1)!})
à vérifier
----------------------------------
______________________________ tu multiplies toutes ces égalités membre à membre
Après tu peux essayer de simplifier des trucs parce que
et
donc on peut écrire le résultat :
Re: suite integral
par MMu » 17 Jan 2016, 21:02
i7ayabaklouti a écrit:Merci beaucoup tu m'a sauver
Remember : Omar m'a tuer :
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :