Exercice sur les suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

 par ayarajaayassmine » 08 Jan 2016, 23:23
par ayarajaayassmine » 08 Jan 2016, 23:23

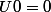
1- montrer que

2- Montrer que Un est strictement croissante
3- Montrer que :
\leq \frac{1}{2}\left(4-Un \right))
déduire
^n \right)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 09 Jan 2016, 08:58
par Carpate » 09 Jan 2016, 08:58
ayarajaayassmine a écrit:
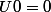
1- montrer que

2- Montrer que Un est strictement croissante
3- Montrer que :
\leq \frac{1}{2}\left(4-Un \right))
déduire
^n \right)
Bonjour,
L'indication de ce que tu as fait ne ferait pas de mal
Je suppose que la suite est
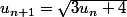
1) le montrer par récurrence
2)
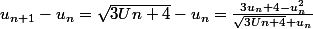
qui est du signe du trinôme du second degré :

lequel est positif "entre ses racines" : -1 et 4 donc positif strict d'après la question 1)

 par ayarajaayassmine » 10 Jan 2016, 01:50
par ayarajaayassmine » 10 Jan 2016, 01:50
Bonjour et merci
C'est surtout les 2 dernières questions qui me posent pb.
Montrer que :
)
et déduire :
^n \right)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Jan 2016, 07:59
par Carpate » 10 Jan 2016, 07:59
Je ne comprends pas pourquoi cet énoncé est si calculatoire pour montrer que (U_n) admet 4 pour limite
On a montré que (U_n) est croissante et majorée (par 4)
Elle admet donc une limite l (positive)
Au passage à la limite (n --> infini),
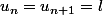
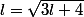
l est la racine positive de
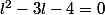
soit
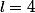
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 10 Jan 2016, 08:46
par nodgim » 10 Jan 2016, 08:46
Tout à fait Carpate, mais l'énoncé est ainsi fait qu'il ne fait pas le raccourci par le calcul direct de la limite. Il fait découvrir la limite d'une autre façon.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Jan 2016, 10:12
par Carpate » 10 Jan 2016, 10:12
Suite du feuilleton ...
}{4+\sqrt{3u_n+4}})
(x par quantité conjuguée)
Pour rester fidèle à l'énoncé il faudrait montrer que

Mais ce n'est pas très facile.
Par contre montrer que

est presque immédiat et suffisant pour la question suivante :


}{8}<\frac{3(4-u_n)}{4+\sqrt{3u_n+4}}\leq\frac34(4-u_n))
) Inégalité que l'on écrit pour n = 1 à n :
Inégalité que l'on écrit pour n = 1 à n :)
)
soit
^2( 4-u_0))
...........................
^n(4-u_0))
Quand
^n \rightarrow 0)
et

-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 10 Jan 2016, 11:00
par nodgim » 10 Jan 2016, 11:00
Hum...C'est bien compliqué tout ça....
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Jan 2016, 12:07
par Carpate » 10 Jan 2016, 12:07
nodgim a écrit:Hum...C'est bien compliqué tout ça....
Et que proposes-tu de plus simple ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Jan 2016, 12:56
par Ben314 » 10 Jan 2016, 12:56
Carpate a écrit:Je ne comprends pas pourquoi cet énoncé est si calculatoire pour montrer que (U_n) admet 4 pour limite
On peut quand même répondre que l'inégalité demandée montre non seulement que la limite est 4, mais donne aussi une idée de la vitesse de convergence.
Par exemple, ça permettrait de répondre à des question (archi. classique) du style "donner une valeur de n telle que Un soit proche de la limite à 10^-3 prés".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 10 Jan 2016, 13:07
par nodgim » 10 Jan 2016, 13:07
Le 3) demande de vérifier que 4-U(n+1)<=1/2(4-Un)
4-V(3Un+4)<=(4-Un)/2
4-(4-Un)/2<=V(3Un+4)
(4+Un)/2<=V(3Un+4)
4+Un<=2V(3Un+4) avec Un > 0
(4+Un)² <= 4(3Un+4)
16+8Un+Un² <= 12Un+16
Un²-4Un <= 0
Un (Un-4) <= 0
Or 0 < Un < 4 a été démontré, donc l'inégalité est vérifiée.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Jan 2016, 13:13
par Ben314 » 10 Jan 2016, 13:13
Sinon,
 & \Leftrightarrow & 4-\sqrt{3U_n+4}\leq 2-\frac{1}{2}U_n\ \ &\cr<br />& \Leftrightarrow & 2+ \frac{1}{2}U_n \leq \sqrt{3U_n+4}\ \ \ \ \ \ \ &\cr <br />& \Leftrightarrow & (2+ \frac{1}{2}U_n)^2 \leq 3U_n+4\ \ \ \ \ \ \ &\text{car }2+ \frac{1}{2}U_n\geq 0\cr <br />& \Leftrightarrow & 4+2U_n+\frac{1}{4}U_n^2 \leq 3U_n+4&\cr <br />& \Leftrightarrow & 0\leq U_n-\frac{1}{4}U_n^2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ &\cr <br />& \Leftrightarrow & 0\leq \frac{1}{4}U_n(4-U_n)\ \ \ \ \ \ \ \ \ \ \ \ &\cr <br />\end{matrix})
EDIT : Nodgim a été plus rapide (mais c'est moins peaufiné...

)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 10 Jan 2016, 14:26
par Pseuda » 10 Jan 2016, 14:26
[/code]
Carpate a écrit:Suite du feuilleton ...
}{4+\sqrt{3u_n+4}})
(x par quantité conjuguée)
Pour rester fidèle à l'énoncé il faudrait montrer que

Mais ce n'est pas très facile.
Et bien, utiliser : pour tout n, 0

, donc

, etc...
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Jan 2016, 19:15
par Carpate » 11 Jan 2016, 19:15
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 123 invités
(x par quantité conjuguée)