bonjour a tous! j'aurai besoin d'aide pour un exercice sur les récurrences je l'ai en partie fai mais j'aurai besoin de votre aide pour me corriger :)
exercice 1/
Soit I=[0;1] On considere la fonction f définie sur I par :
f(x) = (3x+3)/(x+5)
On définit la suite (Un) par Uo=0 et Un+1 = f(Un) pour tout entier naturel n.
1/ Etudier les variations de la fonction f et en déduire que pour tout x de I, f(x) appartient a I
Mon travail personnel :
f est dérivable en I en tant que quotient de fonctions dérivables sur I=[0;1] dont le dénominateur ne s'annule pas sur I=[0;1]
(x+5=0) <=> (x=-5)
f=u/v avec u'(x) = 3 ; v'(x) = 1 ; u(x) = 3x+3 et v(x) = x+5
f'(x) = 12/(x+5)² (apres tout les calculs...)
Le sens de variation est donné par le signe de f'(x), pour tout x de I ; f'(x)>0 donc f est strictement croissante sur I=[0;1]
2/Montrer en utilisant un raisonnement par récurrence que pour tout entier naturel n, Un appartient a I
Travail personnel : On note P(n) la propriété
"(3n+3)/(n+5) appartient a I "
Initialisation :
pour n = 0
(3*0+3)/(0+5)=3/5 appartient a I
Hérédité :
On suppose P(k) vraie pour un certain entier k, c'est a dire qu'on suppose que (3k+3)/(k+5) appartienne a I
Montrons que P(k+1) est vraie, c'est a dire montrons que (3(k+1)+3)/((k+1)+5) appartienne a I
par conséquent (3(k+1)+3)/((k+1)+5) = (3k+6)/(k+6)
voilà et là je bloque pour la suite :( pouvez vous m'aider ?
3/établir la relation Un+1 - Un = [(1-Un)(Un+3)]/(Un+5)
4/ En déduire le sens de variations de la suite.
merci d'avance pour votre aide ! ;)
Récurrence
3 messages
- Page 1 sur 1
Bonjour
Initialisation :
pour n = 0,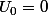 donc
donc 
Hérédité :
On suppose P(k) vraie pour un certain entier positif k, c'est à dire qu'on suppose que appartienne à I.
appartienne à I.
Montrons que P(k+1) est vraie, c'est a dire montrons que
Tu n'as pas terminé la question.destrukt a écrit:1/ Etudier les variations de la fonction f et en déduire que pour tout x de I, f(x) appartient a I......................
donc f est strictement croissante sur I=[0;1]
Non : On note P(n) la propriété
2/Montrer en utilisant un raisonnement par récurrence que pour tout entier naturel n, Un appartient a I
Travail personnel : On note P(n) la propriété
"(3n+3)/(n+5) appartient a I "

Initialisation :
pour n = 0,

Hérédité :
On suppose P(k) vraie pour un certain entier positif k, c'est à dire qu'on suppose que
 appartienne à I.
appartienne à I.Montrons que P(k+1) est vraie, c'est a dire montrons que

3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
