Somme

[teamprepa]

bonjour quelqu'un aurait une piste pour calculer ?

Merci

[Robot]

Tu as toutes les indications nécessaires dans ce fil

Edit : je n'avais pas vu la factorielle. Mais es-tu bien sûr de l'énoncé ? Sur les-mathématiques.net tu donnes un énoncé différent.

[teamprepa]

Tu as toutes les indications nécessaires dans ce fil

dans ce fil on aboutissait sur une série géométrique ce qui n'est pas le cas ici car en passant aux exponentielle on a

[Robot]

C'est la factorielle de ou la factorielle de ? Faudrait savoir !

C'est la somme finie que tu as à calculer, ou la somme de la série ?

Remarque additionnelle : la série ne te dit rien ?

[teamprepa]

C'est la factorielle de ou la factorielle de ? Faudrait savoir !

C'est la somme finie que tu as à calculer, ou la somme de la série ?

Remarque additionnelle : la série ne te dit rien ?

désolée pour mon erreur je suis nouvelle dans l'utilisation de ce language, je fais de mon mieux..
Oui c'est la série exponentielle.

= + =+ = =


Je peux avoir des avis sur ce que j'ai fais svp

[Robot]

désolée pour mon erreur je suis nouvelle dans l'utilisation de ce language, je fais de mon mieux..
Oui c'est la série exponentielle.

= + =+ = =


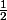
Je peux avoir des avis sur ce que j'ai fais svp

Tu n'as pas répondu sur "somme finie ou somme de la série". Sur les-mathematiques.net tu affirmes que c'est la somme finie, mais vu le résultat ça ne paraît pas très sérieux.
Ce n'est pas la série exponentielle, mais la partie paire de a série exponentielle. Et la partie paire de l'exponentielle, ce n'est pas cosinus mais ...

[teamprepa]

c'est la somme de la série que je dois trouver c'est pour ça qu'au début je pensais passer par les sommes partielles

[aymanemaysae]

Je crois - sauf avis contraire de M. Robot - qu'on a :

= = +

= (ch() + ch()) = cos(sin(x)) ch((cos(x)) : résultat vérifié avec wolfram alpha.


L'erreur était là, et il aurait été suffisant de l'indiquer, comme le font tous les professeurs.
= (ch() + ch()) = ch() .

[Robot]

Tu t'es trompé. Et en plus, c'est l'exo de teamprepa, laisse le faire.

[teamprepa]

Merci de ton aide aymanemaysae je vais exploiter cette piste

[aymanemaysae]

Je vois que tu as une dent contre moi M. robot. Je suis désolé pour toi, dorénavant je ferai comme si tu n'existes pas.

[Robot]

Je te signale que tu fais une erreur (l'as tu vue ?), et je te rappelle que la philosophie du forum n'est pas de faire les exercices à la place des questionneurs.
Si ça te vexe, tant pis pour toi.

[aymanemaysae]

Le néant, n'existe pas, et malgré cela je dis que les mathématiques peuvent se passer de l'impolitesse de quelques mathématiciens et progresser.

[Robot]

En quoi ai-je été impoli ?
En te disant que tu as fait une erreur ? (Tu ne l'as toujours pas vue ?)
En te rappelant que, selon la charte du forum, on ne fait pas un exercice à la place du questionneur ?

[teamprepa]

J'ai apporté des modifications, en me basant sur la formule =ch()*ch()





= = +

= (ch() * (ch()))

[Robot]

Tu as transformé un en ?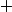
Même en corrigeant ça, tu as progressé mais tu n'es pas tout à fait au bout du chemin.

Je constate qu'aymane... modifie son message au fur et à mesure, mais il laisse encore une grosse erreur :

(ch() + ch() = (ch() + ch()) = ch() .

edit : il a fini par la trouver. Espérons que cette recherche d'erreur lui aura été profitable !

[teamprepa]

= = +

= (ch() * (ch()))=*(ch()))

[teamprepa]

Par contre (ch()) comment je pourrais le simplifier.. Pour que ça soit du sinus il manque le i au denominateur..

[Robot]

Si a est un réel, que vaut ch(ia) ? (Revenir à la définition de ch).

[aymanemaysae]

Introduisez le 'i' et vous obtiendrez le cosinus hyperbolique de (i sin(x)) et en développant le cosinus hyperbolique en exponentielle vous obtiendrez le résultat.

je vous souhaite bon courage et je vous remercie car avec cet exercice j'ai constaté qu'on pouvait faire beaucoup de choses avec les séries trigonométriques.