Trigonalisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 02 Jan 2016, 14:36
par Rik95 » 02 Jan 2016, 14:36
Robot a écrit::cry: M'enfin ??? Tu devrais tout de même être capable de vérifier tout seul que si
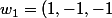)
et
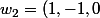)
, alors
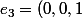 \in \mathrm{Vect(w_1,w_2))
, non ?
Et j'ai déjà expliqué comment compléter une base ....
Enfaite je rectifie pour e3 je trouve a=b et c=-a=-b sa ne fais donc pas l'affaire
Parcontre pour e2 cela fonctionne donc w1 = (1 -1 -1) , w2 = ( -1 1 0) et w3 = (0 1 0 ) forme une base
et j'ai u(w3) = 4w1 + 2w2
Parcontre je ne sais toujours pas comment trouver u(w2), est ce que se serai (-2w2)² ?
-
Robot
 par Robot » 02 Jan 2016, 14:43
par Robot » 02 Jan 2016, 14:43
Tu te mets à écrire n'importe quoi ! Le carré d'un vecteur ?
Tu as une base
)
, tu as un vecteur
)
que tu connais. Tu n'arrives pas à le décomposer dans la base
)
? Ressaisis-toi !
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 02 Jan 2016, 15:00
par Rik95 » 02 Jan 2016, 15:00
Robot a écrit:Tu te mets à écrire n'importe quoi ! Le carré d'un vecteur ?
Tu as une base
)
, tu as un vecteur
)
que tu connais. Tu n'arrives pas à le décomposer dans la base
)
? Ressaisis-toi !
Justement je ne sais pas a quoi est egal u(w2) ?
J'ai pu decomposer u(w3) car je sais que u(e2) = (2 -2 -4) mais aucune idée pour u(w2)
-
Robot
 par Robot » 02 Jan 2016, 15:05
par Robot » 02 Jan 2016, 15:05
Rik95 a écrit:Justement je ne sais pas a quoi est egal u(w2) ?
Euh, tu te fiches de moi ? Tu as

, tu as la matrice de

dans la base canonique :

, et tu prétends ne pas savoir calculer
)
?
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 02 Jan 2016, 15:18
par Rik95 » 02 Jan 2016, 15:18
Robot a écrit:Euh, tu te fiches de moi ? Tu as

, tu as la matrice de

dans la base canonique :

, et tu prétends ne pas savoir calculer
)
?
Apres quelques recherche, je pense avoir compris comment faire il me suffit de calculer le produit -_-
J'ai donc u(w2) = (0 0 2 ) = -2w1 -2w2
Je peu donc ecrire ma matrice T :
-2 -2 4
0 -2 2
0 0 -2
C'est bien sa ?
Parcontre il y'a une chose que je n'ai pas encore compris, pour w2 on l'a chercher dans le ker de (u+2i)², dans quel cas en général est ce que l'on recherche un vecteur de cette façon ?
Ps : merci pour ta patience avec moi, il est vrai que j'ai pas mal de lacunes

-
Robot
 par Robot » 02 Jan 2016, 15:30
par Robot » 02 Jan 2016, 15:30
Ce n'est pas
sa, c'est
ça.
Pour ton questionnement, j'ai déjà répondu. Je rappelle, en explicitant un peu plus :
Robot a écrit:Suppose que la matrice de

est triangulaire dans la base
)
. Montre que :
1°) tous les coefficients diagonaux de cette matrice triangulaire sont
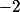
;
2°)
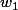
est vecteur propre de valeur propre associée
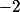
, c.-à-d.
)
.
3°)
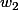
est dans
^2))
.
Si tu avais fait ce que j'ai indiqué, tu devrais comprendre pourquoi on cherche
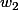
dans
^2))
.
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 02 Jan 2016, 16:03
par Rik95 » 02 Jan 2016, 16:03
Robot a écrit:Ce n'est pas
sa, c'est
ça.
Pour ton questionnement, j'ai déjà répondu. Je rappelle, en explicitant un peu plus :
Si tu avais fait ce que j'ai indiqué, tu devrais comprendre pourquoi on cherche
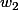
dans
^2))
.
J'ai fait quelques recherche et j'ai trouvé ceci
http://www.mathlaayoune.webs.com/lineaire/reduction/commenttrigonaliserunematricedordretrois.html Si j'ai bien compris la méthode selon le lien, on a trouvé que la dimension de l'espace propre de la valeur propre -2 est egal a 1 < 3 donc c'est pour cela que l'on a calculer ker(u+2i)²
Selon ce raisonnement on aurai egalement pu calculer w3 en passant par ker(u+2i)^3 non ?
-
Robot
 par Robot » 02 Jan 2016, 16:07
par Robot » 02 Jan 2016, 16:07
C'est inutile.
Tu ferais mieux de lire un manuel sérieux plutôt que d'aller à la pêche sur internet, où on peut trouver le meilleur et le pire.
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 02 Jan 2016, 16:17
par Rik95 » 02 Jan 2016, 16:17
Robot a écrit:C'est inutile.
Tu ferais mieux de lire un manuel sérieux plutôt que d'aller à la pêche sur internet, où on peut trouver le meilleur et le pire.
En effet je trouve plus simple la méthode qu'on a utiliser

Est ce que le principe reste le meme pour les matrices 2x2 4x4 .. ect ?
Aussi j'aurai une autre question dans le cas ou on aurai trouver 3 valeurs propre ainsi que 3 espaces propre, on se serai retrouver dans un cas de diagonalisation non ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
et
, alors
, non ?
