Exo TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
camts
- Membre Naturel
- Messages: 12
- Enregistré le: 27 Sep 2015, 17:25
-
 par camts » 02 Jan 2016, 11:33
par camts » 02 Jan 2016, 11:33
Partie A
3/ Démontrer que : ;) x ;) ;), on a : ;)(x² + 1) > |x|
4/ En déduire que : ;) x ;) ;), on a : x < ;)(x² + 1)
Bonjour je bloque sur ces deux questions, quelqu'un pourrait m'aider svp
et aussi sur celle-là
On considère la fonction f définie sur ;) par : f(x) = ;)(x² + 1) ;) x
1/ Montrer que : ;) x ;) ;), on a : f(x) = 1/(x+ ;)(x²+1))

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Jan 2016, 11:44
par zygomatique » 02 Jan 2016, 11:44
salut
la fonction racine est croissante ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
camts
- Membre Naturel
- Messages: 12
- Enregistré le: 27 Sep 2015, 17:25
-
 par camts » 02 Jan 2016, 11:46
par camts » 02 Jan 2016, 11:46
zygomatique a écrit:salut
la fonction racine est croissante ...
Je comprend pas ce que je peux faire avec ça

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Jan 2016, 12:15
par zygomatique » 02 Jan 2016, 12:15
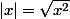
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
camts
- Membre Naturel
- Messages: 12
- Enregistré le: 27 Sep 2015, 17:25
-
 par camts » 02 Jan 2016, 12:46
par camts » 02 Jan 2016, 12:46
zygomatique a écrit: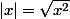
...
|x| = \sqrt {x^2}
donc \sqrt {x^2}+1 > |x|
c'est ca ?
et du coup je fais quoi pour la deux ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Jan 2016, 13:48
par zygomatique » 02 Jan 2016, 13:48
|x| = \sqrt {x^2} donc \sqrt {x^2}+1 > |x|
ce
donc est un peu rapide
pour tout x :: x =< |x|
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
