Série

[teamprepa]

Bonjour, je dispose de la séérie de terme générale : 1/2^n *cos(nx)
Je dois trouver la somme de la série lorsque x=pi

J'ai trouvé -2 pouvez vous me le confirmer svp?

Merci d'avance

[Robot]

J'infirme !
Same player shoot again !

[teamprepa]

J'infirme !
Same player shoot again !

Pouvez vous m'expliquer pourquoi svp

[Robot]

Comment as-tu trouvé -2 ?

[teamprepa]

Comment as-tu trouvé -2 ?

cos(n*pi)=-1

donc somme de 0 à + l'infini de 1/2^n *cos(n*pi)=somme de 0 à + l'infini de -1/2^n en utilisant la formule de la somme pour les séries géométrique je trouve -1/(1-(1/2))=-2

[Robot]

cos(n*pi)=-1

Hum... Pour n=0 ? Pour n= 2 ?

[teamprepa]

Hum... Pour n=0 ? Pour n= 2 ?

Oui j'ai remarqué que ça fonctionne que pour les n impairs mais pour les n pairs ça fait 0. Du coup je ne sais pas comment formuler la réponse..

Vous avez une idée

[Robot]

mais pour les n pairs ça fait 0.

Ah bon ? ?

[teamprepa]

Ah bon ? ?

autant pour moi ça fait 1 du coup la somme serait de 2 si j'ai bien compris?

Donc est ce que je peux dire que ma somme en pi vaut (-1)^n * 2 ?

[Robot]

Réfléchis un peu avant d'écrire n'importe quoi !

[teamprepa]

Réfléchis un peu avant d'écrire n'importe quoi !

Pourtant cos(0)=1 ce qui nous laisse

ce qui nous donne 2..

[Robot]

Une bonne fois pour toute, que vaut ?
Commence par regarder , , , .

Je renouvelle mon conseil : une bonne sieste ! Tu feras sans doute moins de bêtises après.

[teamprepa]

Une bonne fois pour toute, que vaut ?
Commence par regarder , , , .

=1
=-1
=1
=-1

Lorsque n est pair on a 1 lorsque n est impair -1
Ce qui donne pour la somme :

- pour les n pairs :



- pour les n impairs:

[Ben314]

Ton truc du "pour n pair" et "pour n impair" ne veut absolument rien dire...
Normalement, ça fait un moment que tu aurais du comprendre qu'une expression de la forme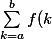 , elle dépend de , de etde la fonciton , mais absolument pas de k vu que c'est une abréviation pour dans laquelle la lettre k n'apparait pas.
Pour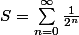 , c'est un soupçon plus vicieux, vu que, par définition, 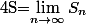où dépend effectivement de n.
Sauf que j'espère qu'en post-bac, tu as fini par comprendre que la limite d'une suite lorsque n tend vers l'infini, ben lui elle, elle ne dépend plus de n.

En bref, ton truc, ça vaut zéro pointé vu que ta somme ne dépend pas de n !!!

Si tu tient absolument à regrouper les + ensemble et les -, ben tu écrit par exemple que

[teamprepa]

ok maintenant je comprends pourquoi c'est pas bon.. MERCI!