Suite de cauchy

[souhailamir]

bonjours
svp qui peut montrer que la suite fn(x)=racine((x^2)+1/n) est de cauchy ??

[Robot]

Le patronyme d'Augustin Louis Cauchy (1789-1853) commence par une majuscule.
Ensuite, tu ne nous dis pas dans quel espace habite . En particulier, quelle est la norme ?

[souhailamir]

Le patronyme d'Augustin Louis Cauchy (1789-1853) commence par une majuscule.
Ensuite, tu ne nous dis pas dans quel espace habite . En particulier, quelle est la norme ?

pardon;
pour l espace C^1([-1,1]) munit la norme de la convergence uniforme.

[Robot]

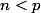
Essaie de majorer , pour , en fonction de uniquement.

[mathelot]

pardon;
pour l espace C^1([-1,1]) munit la norme de la convergence uniforme.

n'est pas complet

[Robot]

Et alors ?
Visiblement, la question à laquelle souhailamir essaie de répondre est une étape dans la démonstration de ce fait.

[souhailamir]

Et alors ?
Visiblement, la question à laquelle souhailamir essaie de répondre est une étape dans la démonstration de ce fait.

oui,c'est vrai

[Robot]

Bon, tu as progressé ?

[ilikoko123]

Et alors ?
Visiblement, la question à laquelle souhailamir essaie de répondre est une étape dans la démonstration de ce fait.

Voulez vous dire que la suite est de cauchy sans être convergente ? par contre je vois que |x| est une limite uniforme de la suite de fonction sur [-1,1]

[ilikoko123]

Non ! Je m'excuse , j ai oublié la condition que la limite ne doit pas sortir de l'espace

[Robot]

Pourquoi cette manie de priver Cauchy de sa majuscule ?

[souhailamir]

Bon, tu as progressé ?

est ce que la majoration suivant est vrai ?
<1/racine(n) .
c'est vrai alors (fn) est de Cauchy qui ne converge pas dans E ,finalement E n'est pas de Banach.

[Robot]

La majoration est correcte, mais un résultat sans les arguments ne renseigne pas sur la justesse de la démarche.