Problèmes pour les transformations de Laplace !

[Nekqlkfhsjkdh]

Bonjour !

Je n'arrive pas à trouver la solution de la transformation de Laplace pour cette équation différentielle :

y'' + alpha* y' = H(t)*e^(-at) sachant que y(0)=0 et y'(0)= 0

Je bloque au moment de l'identification, je ne sais pas si je décompose bien le dénominateur. Quelqu'un pourrait me donner une solution ?

Merci d'avance !

[Pisigma]

Bonjour !

Je n'arrive pas à trouver la solution de la transformation de Laplace pour cette équation différentielle :

y'' + alpha* y' = H(t)*e^(-at) sachant que y(0)=0 et y'(0)= 0

Je bloque au moment de l'identification, je ne sais pas si je décompose bien le dénominateur. Quelqu'un pourrait me donner une solution ?

Merci d'avance !

Bonsoir,

Montre un peu tes calculs.

As-tu plus de détails sur H(t)?

[Sake]

Salut,

Bonsoir,

Montre un peu tes calculs.

As-tu plus de détails sur H(t)?

Je pense que c'est un Heaviside, du coup il passe à la trappe quand on passe à la transfo de Laplace, et on obtient un classique 1/(a + p) pour peu que Re(a + p) > 0.

[Nekqlkfhsjkdh]

Bonsoir,

Montre un peu tes calculs.

As-tu plus de détails sur H(t)?

Pour H(t)e^-at je le transforme en 1/(a+p)

Donc je me retrouve avec ça :

Y(p) * (p^2+ alpha*p) = 1/(a+p)
Y(p) = 1/(p^2+alpha*p)(a+p)

j'ai décomposé ainsi :

= A/(a+p) + B/p + C/(p+alpha)

je trouve après développement

A+B+C = 0
A*alpha + B*a + B*alpha + C*a = 0
B*a*alpha = 1

Et je trouve des trucs compliqués après je sais pas trop quoi faire pour m'en sortir.

Voilà, voilà !

[Pisigma]

Salut,

Je pense que c'est un Heaviside, du coup il passe à la trappe quand on passe à la transfo de Laplace, et on obtient un classique 1/(a + p) pour peu que Re(a + p) > 0.

çà m'a échappé car souvent on la note U(t)

[Pisigma]

Pour H(t)e^-at je le transforme en 1/(a+p)

Donc je me retrouve avec ça :

Y(p) * (p^2+ alpha*p) = 1/(a+p)
Y(p) = 1/(p^2+alpha*p)(a+p)

j'ai décomposé ainsi :

= A/(a+p) + B/p + C/(p+alpha)

je trouve après développement

A+B+C = 0
A*alpha + B*a + B*alpha + C*a = 0
B*a*alpha = 1

Et je trouve des trucs compliqués après je sais pas trop quoi faire pour m'en sortir.

Voilà, voilà !

Sauf erreur de ma part et en procédant comme suit (il existe d'autres méthodes):



En identifiant terme en

Si ,

Si ,

dans (1) donne

[Nekqlkfhsjkdh]

Je ne comprend pas pour quoi par identification c'est égale à 1 par identification pour p^2 je comprend que ce soit 0 et qu'on est A+B+C = 0 mais pour les autres je ne comprend pas..

[Ben314]

Salut,
Tu veut que pour tout réel p

Et là, il y a plusieurs méthode :

- Soit tu développe et tu utilise le théorème qui dit que, pour que deux polynômes soient égaux sur R, il faut et il suffit qu'ils aient les même coefficients (ce que certains appellent "par identification", mais il faut bien être conscient que c'est un théorème pas complètement évident qu'il y a derrière)

- Soit tu sait d'avance qu'il y a des solutions (est-ce le cas ?) et, vu que l'égalité en question doit être vrai pour n'importe quel réel p, tu prend quelques valeurs particulières de p pour voir ce que donne l'équation dans ce cas là.
Si on a un minimum d'astuce (dans le choix des valeurs de p), c'est souvent plus rapide comme ça. Par exemple ici, considérer les 3 cas particuliers p=0, p=-a et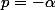 donne rapidement la solution.