Coordonées d'un vecteur

[mogow29]

Bonsoir, est ce que vous pouvez m'aider pour mon exercice de maths ?

On donne les points A(-3;2) B(2;4) et C(5;-3)

Dans chacun des cas suivants, trouvez les coordonnées (xM;yM) du point M.
1. ABCM est un parallélogramme.
2. M est le point de l'axe des abscisses tel que les vecteurs et sont colinéaires.
3. M est l'image de C par la symétrie de centre B

Merci beaucoup de votre aide.

[kso29]

Bonsoir, est ce que vous pouvez m'aider pour mon exercice de maths ?

On donne les points A(-3;2) B(2;4) et C(5;-3)

Dans chacun des cas suivants, trouvez les coordonnées (xM;yM) du point M.
1. ABCM est un parallélogramme.
2. M est le point de l'axe des abscisses tel que les vecteurs et sont colinéaires.
3. M est l'image de C par la symétrie de centre B

Merci beaucoup de votre aide.

Bonsoir,
Pour la 1)
je te conseille de faire un dessin au brouillon un parallélogramme en plaçant bien les lettres (sans les croiser). On étudie donc les vecteurs
et par exemple.
il faut calculer les coordonées, Pour AB c'est (xB-xA;yB-yA)=> (5;2)
puisque ABCM est un parallélogramme, les vecteurs
et ont les MEMES coordonnées.

Ainsi, (5-xM;-3-yM) car C (5;-3)
on en déduit que MC (5;2) et donc que M(0;-5)

Pour la 2) je pense qu'il faut se servir de la condition de colinéarité c-à-d si xy'=x'y pour les vecteurs AB et CM bien sûr. De plus on remarque que pour M, seule son abscisse change, son ordonnée sera toujours égale à 0 puisqu'il se trouve sur l'axe des abscisses. donc
AB(5;2)
CM(xM-5;0-(-3))=> (xM-5;3)
5*3=2*xM-5
15=2*(xM-5)
xM=(15/2)+10=25/2
M(25/2;0)

Pour la 3) il faut appliquer la formule des milieux des vecteurs:
(ici B est le milieux de )
xB=(xC+xM)/2

yB=(yC+yM)/2

On connait B donc:
2=(5+xM)/2 =>xM=4-5=-1
4=(-3+yM)/2=>yM=8+3=11
donc M(-1;11)

Voila ! :lol3:

[siger]

bonjour

qui est supposé faire l'exercice, mogow29 ou kso29 ?

bonne année a venir ......

[mogow29]

bonjour

qui est supposé faire l'exercice, mogow29 ou kso29 ?

bonne année a venir ......

Logiquement c'est à moi de répondre et même avec ses explications je n'ai pas compris la 1).

[siger]

re

quand deux vecteurs sont paralleles leur coordonnees sont proportionnelles
AB est parallele et egal a CD si
(xB-xA )/(yA-yB)=(xD-xC)/(yD-yC)

un quadrilatere est un ABCM est un parallelogramme si deux cotes opposes sont paralleles et egaux soit si ( en vecteurs)
AB =CM
connaissant les coordonneesde A,B et C on en deduit les coordonnees de M
........

[laetidom]

Logiquement c'est à moi de répondre et même avec ses explications je n'ai pas compris la 1).

Bonjour mogow29,

1) Si tu es d'accord avec ce que t'a dit siger dans le post précédent, c'est-à-dire que , tout en regardant la figure ci-jointe :http://www.cjoint.com/c/ELDr7bMiWDf, je pense que tu peux comprendre que pour trouver les coordonnées de M, pour que ABCM soit un parallélogramme,...

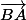
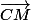
..., en fait, il suffit d'opérer le même déplacement que celui qui consiste de passer de B vers A (par le vecteur ) mais à l'endroit qui nous intéresse, c'est-à-dire de C vers M (par le vecteur qui est égal à ).

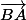
donc opérer, comme tu vois sur la figure jointe, une translation horizontale de - 5 unités puis une translation verticale de - 2 unités :



donc si tu es en C ( 5 ; -3) :

c'est-à-dire en x=5 tu appliques à 5 un déplacement de - 5 donne 5 -5 = 0

c'est-à-dire en y=-3 tu appliques à -3 un déplacement de - 2 donne -3 - 2 = - 5

ce qui veut dire que M(0 ; -5)

en espérant que cela suffira.


Bonne soirée.





nota : translation veut dire déplacement