Calcul de primitive
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Plimpton
- Membre Naturel
- Messages: 86
- Enregistré le: 27 Sep 2015, 14:41
-
 par Plimpton » 28 Déc 2015, 21:20
par Plimpton » 28 Déc 2015, 21:20
Bonsoir à tous !
J'aurais besoin d'aide pour déterminer une primitive. Elle est sous la forme

. Je n'ai pas trouvé la formule de la primitive d'une racine carrée, dans les livres que j'ai. Plus précisément, j'aimerais calculer la primitive de

, pour calculer une intégrale. Les recherches que j'ai faites m'ont donné une formule avec un arcsinus, ce qui me parrait très bizarre vu qu'on parle de racine carrée. Savez-vous si il y a réellement un arcsinus dans la primitive, et si oui, sauriez-vous expliquer pourquoi ?
Merci d'avance !

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 28 Déc 2015, 21:41
par WillyCagnes » 28 Déc 2015, 21:41
bsr
oui il y a un arcsinus
[url=http://www.wolframalpha.com/input/?i=int+%281-x^2%29^0.5&lk=4&num=1&lk=4&num=1]http://www.wolframalpha.com/input/?i=int+%281-x^2%29^0.5&lk=4&num=1&lk=4&num=1[/url] bsr
sinon tu poses x=sin(u)
dx=cos(u)du
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 28 Déc 2015, 21:56
par Pisigma » 28 Déc 2015, 21:56
Plimpton a écrit:Bonsoir à tous !
J'aurais besoin d'aide pour déterminer une primitive. Elle est sous la forme

. Je n'ai pas trouvé la formule de la primitive d'une racine carrée, dans les livres que j'ai. Plus précisément, j'aimerais calculer la primitive de

, pour calculer une intégrale. Les recherches que j'ai faites m'ont donné une formule avec un arcsinus, ce qui me parrait très bizarre vu qu'on parle de racine carrée. Savez-vous si il y a réellement un arcsinus dans la primitive, et si oui, sauriez-vous expliquer pourquoi ?
Merci d'avance !
Bonsoir,

Pose
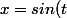, dx=cos(t)dt)
dt=\int\dfrac{1+cos(2t)dt}{2}=\dfrac{t}{2}+\dfrac{sin(2t)}{4}+C)
En repassant aux x
}{2}+\dfrac{sin(2 arcsin(x)}{4}+C=\dfrac{arcsin(x)}{2}+\dfrac{x\sqrt{1-x^2}}{2}+C)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 29 Déc 2015, 03:05
par Ben314 » 29 Déc 2015, 03:05
Salut,
Un petit rappel : si
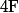
est une primitive de

sur [a,b] alors
dt=F(b)-F(a))
et, dans l'autre sens, on peut définir une primitive de f en posant
=\int_{a}^xf(t)dt)
.
Donc, par exemple, une des primitive de
=\sqrt{1-x^2})
définie sur [-1,1], est
=\int_{-1}^x\sqrt{1-t^2}dt)
.
Fait un beau dessin sur lequel tu trace la courbe de

puis regarde à quoi correspond la surface sous la courbe entre les droites d'équation x=-1 et x=a où a est un réel fixé de [-1,1]
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Plimpton
- Membre Naturel
- Messages: 86
- Enregistré le: 27 Sep 2015, 14:41
-
 par Plimpton » 29 Déc 2015, 08:19
par Plimpton » 29 Déc 2015, 08:19
Merci ! Si je comprend bien, il n'y a pas de formule générale pour la primitive de

?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 29 Déc 2015, 11:10
par Ben314 » 29 Déc 2015, 11:10
Exactement.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
. Je n'ai pas trouvé la formule de la primitive d'une racine carrée, dans les livres que j'ai. Plus précisément, j'aimerais calculer la primitive de
, pour calculer une intégrale. Les recherches que j'ai faites m'ont donné une formule avec un arcsinus, ce qui me parrait très bizarre vu qu'on parle de racine carrée. Savez-vous si il y a réellement un arcsinus dans la primitive, et si oui, sauriez-vous expliquer pourquoi ?