Soit
On a donc
On cherche simplement la fonction de répartition de
Lorsque
Lorsque
Et donc finalement :
Est-ce exact ?
Joyeux Noël à tous ! :happy:
Transfert de variables aléatoires.
3 messages
- Page 1 sur 1
Transfert de variables aléatoires.
par Utoya » 25 Déc 2015, 11:26
J'ai besoin juste d'une petite correction.
Soit
une variable aléatoire qui suit une loi exponentielle de paramètre 
et 
.
On a donc
la fonction de répartition 
et 
la fonction de répartition de qui vaut : =\begin{cases} 0 & \text{si }0 < x \\ 1 - e^{-\lambda x } & \text{si }x \ge 0 \end{cases})
On cherche simplement la fonction de répartition de.
Lorsque
:
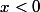
 = P([Y \le x]) = 0)
Lorsque
:
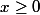
 = P([Y \le x]) = P([{X^3} \le x]) = P([X \le x^{\frac{1}{3}}]) = 1 - e^{-\lambda x^{\frac{1}{3}})
Et donc finalement :
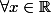
: =\begin{cases} 0 & \text{si }0 < x \\ 1 - e^{-\lambda x^{\frac{1}{3}}} & \text{si }x \ge 0 \end{cases})
Est-ce exact ?
Joyeux Noël à tous ! :happy:
Soit
On a donc
On cherche simplement la fonction de répartition de
Lorsque
Lorsque
Et donc finalement :
Est-ce exact ?
Joyeux Noël à tous ! :happy:
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :