[pluie2]

Bonjour à tous, j'aimerais avoir de l'aide pour cet exercice notamment pour la partie de programmation en langage python:

Pour voyager en bus, un billet vaut 2 euros. Si, pendant un contrôle, le voyageur n'a pas de billet, l'amende est de 30 euros la première fois et 70 euros au deuxième contrôle. On suppose la probabilité de contrôle constante. Un fraudeur décide de ne pas payer ses tickets jusqu'à son deuxième contrôle. Soit X la variable aléatoire indiquant le numéro du voyage au cours duquel a lieu le deuxième contrôle. La probabilité d'effectuer un voyage sans contrôle est q=1-p.

1. Ecrire une fonction simulant l'expérience ci-dessus prenant en argument p et renvoyant une valeur de X.
2. Ecrire une fonction prenant comme arguments un entier k et un réel p de ]0,1[ et renvoyant une valeur approchée de P(X=k).
3. Montrer que pour tout k>=2, P(X=k)=(k-1)p²q^(k-1)

j'ai fait :

1. J'ai écrit un programme m'inspirant d'une loi géométrique en disant que le deuxième contrôle représente le temps d'attente du premier succès. J'obtiens :
def voyage(p):
x=random()
n=1
while x>p:
n=n+1
x=random()
return(n)
2. Ici je ne vois pas comment écrire le programme. On cherche la probabilité que le deuxième controle arrive au voyage n°k mais je ne vois pas comment l'écrire.

3.J'ai écrit que l'événement {X=k}=Xbarre1 et Xbarre2 et ...et Xbarre(k-1) et X_k mais je n'obtiens pas ce qui est demandé

merci de m'aider car je ne comprends pas mes erreurs !

[pluie2]

Faut il introduire une nouvelle variable aléatoire ?

[Ben314]

Salut,
Effectivement, ton résultat n'est pas le bon vu que X c'est le N° du voyage où a lieu le deuxième contrôle alors que ce que tu calcule c'est le N° du voyage où a lieu le premier contrôle.

Pour que le deuxième contrôle ait lieu au k-ième voyage, il faut que la "série des voyages" soit de quel type ?

(et je pense pas qu'il soit utile d'introduire une nouvelle variable)

[pluie2]

en fait j'ai considéré que le deuxième contrôle était le temps d'attente du premier succès donc je me retrouvais avec une loi géométrique.
je ne comprends en revanche pas ce que vous entendez par le type de série, cad géométrique par exemple ?

[Ben314]

en fait j'ai considéré que le deuxième contrôle était le temps d'attente du premier succès ????? donc je me retrouvais avec une loi géométrique.

Donc c'est bien ce que je disait : tu as a évalué le temps pour le premier contrôle et pas pour le second.

Sinon, ce que je voulais dire, c'est qu'à chaque voyage en bus, il y a deux issues possible : contrôlé (C) ou non contrôlé (N) et qu'une série de k voyages, c'est une série de k lettres N ou C.
Pour que X=k, c'est à dire que le deuxième contrôle ait lieu au k-ième voyage, il faut que la série soit de la forme CNN...NNC ou NCN...NC ou NNCN...NC . . . ou NN...NCC (de longueur k à chaque fois)
Vu que les cas sont clairement disjoints, p(X=k) c'est la somme des proba de toutes ces "séries de voyage".

EDIT : en reprenant tes notation avec des Xi barre (ou pas barre...), tu as

[pluie2]

ok je vois mieux le modèle maintenant...

donc si je reprends ça donne:

p(X=k)=(p*q^(k-1-2)*p)+(q*p*q^(k-1-3)*p)+...+(q^(k-2)*p²)
p(X=k)=(p²q^(k-3))+(p²q^(k-3))+...+(q^(k-2)p²)

c'est l'ensemble des termes "+...+" qui me gènent puisque je dois trouver une forme plus générale pour me retrouver avec le résultat de l'énoncé.
je ne vois pas d'où peut sortir le facteur (k-1) de l'énoncé ?

[Ben314]

p(X=k)=(p*q^(k-1-2)*p)+(q*p*q^(k-1-3)*p)+...+(q^(k-2)*p²)
p(X=k)=(p²q^(k-3))+(p²q^(k-3))+...+(q^(k-2)p²)

Les exposants en rouge sont faux.
Par exemple, pour le premier qui correspond à CNNN....NNNC, comme au total il y a k trajet, c'est qu'il y en a k-2 avec des N au milieu.
Idem pour NCNN...NNNC où il y a k-3 fois N dans la série du milieu.
Et de façon générales, dans tout les NN...NCNN...NC il y a k lettres dont deux C donc il y a k-2 N.
Ce qui fait que la deuxième ligne est
p(X=k)=(p²q^(k-2))+(p²q^(k-2))+...+(q^(k-2)p²)
Et tu n'as plus qu'a compter sur tes doigts combien de fois apparaît ce même terme de p²q^(k-2) pour avoir la réponse.

Pour voir si tu comprend le principe, est-ce que tu pourrait me donner p(Y=k) où Y représente le N° du voyage où a eu lieu le troisième contrôle ?
Voir même p(Zq=k) où Zq est le N° du trajet où a lieu le q-ième contrôle ? (avec q fixé et k>=q évidement)

[pluie2]

du coup:

p²q^(k-2) apparait k-1 fois donc on retrouve bien ce qu'il faut montrer (merci :) )

Pour votre exemple:

P(Y=k)=P(X1 et X2 et X3barre et ....et X(k-1)barre et Xk) + P(X1barre et X2 et X3 et ...et Xk)+...+P(X1barre +...+X(k-2)+X(k-1)+Xk)

Au total, il y a toujours k trajets et k-3 au milieu donc P(Y=k)=(k-1)p^3*q^(k-3)

Pour P(Zq=k), je dirais qu'elle vaut: (k-1)*p^q*q^(k-q) ?

[Ben314]

C'est O.K. pour X (de l'énoncé), mais pas pour Y et Z.
Pour p(Y=k) il faut regarder toute les "séries de voyages" de la forme N...NCN...NCN...NC de longueur k, avec un C à la fin et deux autres C n'importe où dans les k-1 premiers trajets.
N'importe quelle série de voyage de ce type a une proba. mais il y a autant de série de voyage de ce type que de façon de tirer 2 éléments parmi k-1 (les emplacement des deux C parmi les k-1 premières positions)
Donc où désigne le coeff. binomial (et il faut évidement que , c'est à dire que )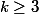

Idem pour où (avec )

[pluie2]

ok je vais essayer de refaire vos exemples car je n'avais pas du tout vu ça comme ça !

Je voulais également programmer cet énoncé en python (algorithme) et plus précisément, programmer la variable aléatoire X pour que le programme me renvoie P(X=k) :
from random import *
def voyage1(p):
x=random()
n=1
while x>p:
n=n+1
x=random()
return(n)

sauf que je me rends compte que j'ai programmé ici une loi géométrique car le return me renvoie le temps d'attente du premier succès. En ignorant le résultat de P(X=k) donné dans l'énoncé, avez vous une idée de comment je pourrais modifier mon programme pour qu'il me modélise la situation ?

[Ben314]

def voyage1(p):
V=0 ; C=0 { 0 voyage ; 0 contrôle)
while C<2:
| V=V+1
| x=random()
| if x

return(V)

[pluie2]

merci beaucoup pour votre aide je vais reprendre tout ça