Bonjour,
je suis actuellement en révision pour mes partiels, et j'ai noté quelques soucis concernant les développements limités.
Merci d'avance pour votre aide.
1) Donner le développement limité de f*g avec:
f(x)=1+2x+x^2+o(x^2)
g(x)=1-x+3x^2+o(x^2)
je trouve et le résultat est bon:
f*g=1+x+2x^2+o(x^2)
c'est la question 2) qui me gène bien qu'elle soit simple:
2)donner le développement limité de 1/f et 1/g.
je pars de (1+2x+x^2+o(x^2))^-1 (inverse) je sais qu'il y a moyen de me ramener à une forme usuelle (1+x) mais je n'y arrive pas, la correction du professeur saute pas mal de ligne :s
Développement limité L1
12 messages
- Page 1 sur 1
Bouji a écrit:justement c'est bien le u qui me dérange, dans certains DL on peut poser X=2x+x^2
Je suppose alors que je peux le faire ici aussi?
Donc en posant X=2x+x^2
J'applique la formule (1+x)^a avec a=-1
donc (1+x)^-1=1-X+X^2+o(x^2)
je trouve 1/f= 1-2x+3x^2+o(x^2)
Je pense que c'est correct ?
Merci.
Je comprends pas qui te dérange puisque tu fais exactement la même chose que je t'ai dite. Qu'entends tu par certains DL? pourquoi retires tu le o(x^2) dans l'écriture de X?
Moi je propose juste d'utiliser le fait suivant:
Si une fonction u admet un DL à 0 à l'ordre n, alors 1/(1+u) admet un DL à 0 à l'ordre n, et ce DL est donné en écrivant 1/(1+u)=1-u+u^2-u^3+....+(-1)^n u^n+o(u^n). et pour avoir l'écriture de u^k tu écris le DL de u, tu prends la partie polynomiale tu l'élèves à la puissance k et tu ne gardes que les termes d'ordre inférieur ou égal à n.
Ton résultat au final est correct
Comme l'a dit M. Moulou, votre résultat est juste, mais je poste ma solution dans l'espoir que M. Moulou veuille bien me corriger sa rédaction.
Soit le développement limité de f au voisinage de 0, et
le développement limité de f au voisinage de 0, et  le développement limité de
le développement limité de 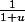 au voisinage de 0, avec
au voisinage de 0, avec  = 1 + 2x +
= 1 + 2x +  + o(
+ o( ) et
) et = 1 - u +
= 1 - u + 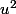 + o(
+ o(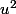 ) .
) .
Si u = f(x) - 1 , alors u = 2x + +o(
+o( ) et
) et 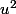 = 4
= 4  + o(
+ o( ), et on peut écrire:
), et on peut écrire:
}) =
= 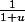 = 1 - ( 2x +
= 1 - ( 2x +  ) + 4
) + 4  + o(
+ o( ) = 1 - 2x + 3
) = 1 - 2x + 3  + o(
+ o( ).
).
Soit
Si u = f(x) - 1 , alors u = 2x +
Finalement ça ne me dérange pas, disons que la correction de mon prof est... incorrect et ça m'a induit en erreur. C'est seulement que j'ai eu du mal à prendre le u, je l'ai fait daprès ton indication.
Pour le o(x^2) c'est une faute de frappe.
Merci beaucoup pour ton aide, c'est bien simple finalement :)
Si j'ai besoin d'aide sur les DL, je peux up ce post ou je dois en re-crée un ?
Pour le o(x^2) c'est une faute de frappe.
Merci beaucoup pour ton aide, c'est bien simple finalement :)
Si j'ai besoin d'aide sur les DL, je peux up ce post ou je dois en re-crée un ?
Faire quand même gaffe que, pour que le o(u^n) soit bien un o(x^n), ça serait assez utile que u(x) "commence" par du lambda.x (i.e. qu'il n'y ait pas de constante)MouLou a écrit:Si une fonction u admet un DL à 0 à l'ordre n, alors 1/(1+u) admet un DL à 0 à l'ordre n, et ce DL est donné en écrivant 1/(1+u)=1-u+u^2-u^3+....+(-1)^n u^n+o(u^n). et pour avoir l'écriture de u^k tu écris le DL de u, tu prends la partie polynomiale tu l'élèves à la puissance k et tu ne gardes que les termes d'ordre inférieur ou égal à n.
Dit autrement, le D.L. 1/(1+u)=1-u+u²..., il est valable pour u proche de 0 donc si on remplace u par un truc, il faut absolument que le truc soit proche de 0.
Je dit ça parce que j'ai déjà vu souvent du
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
aymanemaysae a écrit:Comme l'a dit M. Moulou, votre résultat est juste, mais je poste ma solution dans l'espoir que M. Moulou veuille bien me corriger sa rédaction.
Soitle développement limité de f au voisinage de 0, et
le développement limité de
au voisinage de 0, avec
= 1 + 2x +
+ o(
) et
= 1 - u +
+ o(
) .
Si u = f(x) - 1 , alors u = 2x ++o(
) et
= 4
+ o(
), et on peut écrire:
=
= 1 - ( 2x +
) + 4
+ o(
) = 1 - 2x + 3
+ o(
).
Tu as oublié de préciser à quel ordre tu fais le DL! :--:
Trève de pinaillage c'est comme cela que j'aurais écrit oui.
Ben314 a écrit:Faire quand même gaffe que, pour que le o(u^n) soit bien un o(x^n), ça serait assez utile que u(x) "commence" par du lambda.x (i.e. qu'il n'y ait pas de constante)
Dit autrement, le D.L. 1/(1+u)=1-u+u²..., il est valable pour u proche de 0 donc si on remplace u par un truc, il faut absolument que le truc soit proche de 0.
Je dit ça parce que j'ai déjà vu souvent duqui est complètement incohérent pour x proche de 0, (par contre ça serait valable pour x proche de -1...)
Oui c'est très juste merci de la précision que j'avais oubliée
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
