Transformation linéaire

[Crazyfrog]

Bonsoir tout le monde, je me penche sur un exos:
1. Décrire explicitement une transformation linéaire A : R4 ;) R3 appliquant R4 sur le sous-espace engendré par (2,1,0) et (5,;)1,2), et ayant pour noyau le plan déterminé par les équations x = y = z.
je ne comprends pas bien l'énoncé

[Robot]

On te demande de donner un exemple de matrice à 3 lignes et 4 colonnes (matrice d'une application linéaire de 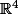dans , dans les bases canoniques), dont l'image est le sous-espace de engendré par les deux vecteurs indiqués (de dimension 2, puisque ces deux vecteurs ne sont pas colinéaires), et dont le noyau est le plan vectoriel (de dimension 2) dans 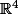décrit par les équations 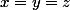. C'est le plan formé par les vecteurs de 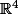dont les trois premières coordonnées sont égales.

Tu remarqueras qu'on est sympa : la dimension de l'image voulue (2) plus la dimension du noyau voulu (2) est bien égal à la dimension de l'espace de départ (4). Pas de contradiction avec le théorème du rang !

[Pierrot73]

ayant pour noyau le plan déterminé par les équations x = y = z.

Il s'agit du plan (donc dim = 2) qui est formé par les vecteurs u de R4 qui sont de la forme (x, x, x, t), puisque x = y = z.

A : R4 R3 appliquant R4 sur le sous-espace engendré par (2,1,0) et (5,;)1,2)

Par la suite, il y a plusieurs façons de décrire ton application. Il faut exprimer l'image de la base de R4, par exemple la base canonique {ei}, avec i de 1 à 4. Tu sais qu'au moins 2 de ces vecteurs seront envoyés sur 0 puisque dim(Ker) = 2. Si tu choisis d'envoyer e1 et e2 sur 0, tu pourras poser : f(e3) = 2*e1 + e2 ; je te laisse faire pour f(e4).

[Edit : Robot a été plus rapide ]

[Ben314]

Il faut exprimer l'image de la base de R4, par exemple la base canonique {ei}, avec i de 1 à 4. Tu sais qu'au moins 2 de ces vecteurs seront envoyés sur 0 puisque dim(Ker) = 2.

Heuuuu..... c'est un tout petit peu n'importe quoi ça.....

[Crazyfrog]

merci de vos réponses
donc par exemple la transformation linéaire (x,y,z,t) ---> (x-y,y-z,0)
qui a pour matrice
1 -1 0 0
0 1 -1 0
0 0 0 0 ?

[Ben314]

Le noyau de cette application est effectivement le plan d'équation x=y=z de R^4 , mais l'image n'est pas la bonne.
Là, l'image est engendré par (1,0,0) ; (-1,1,0) ; (0,-1,0) ; (0,0,0) [les vecteurs colonne de ta matrice]
c'est à dire en fait par (1,0,0) ; (0,1,0) et ça ne correspond pas à l'image souhaitée...

L'idée est bonne quand même, mais il faut rajouter un truc...

[Pierrot73]

Heuuuu..... c'est un tout petit peu n'importe quoi ça.....

Ah bon ? J'ai pourtant eu un exo du même type (R3 dans R2, avec d'autres vecteurs etc) et j'avais eu juste au DM (en tout cas, j'ai eu l'appréciation "vu" que j'ai interprété comme "pas de fautes" puisque les fautes sont barrées ; ou sinon "vu" voudrait dire "suffisamment faux pour que je ne m'embête pas à tout barrer" ?). Je comprends pas

[zaidoun]

Ah bon ? J'ai pourtant eu un exo du même type (R3 dans R2, avec d'autres vecteurs etc) et j'avais eu juste au DM (en tout cas, j'ai eu l'appréciation "vu" que j'ai interprété comme "pas de fautes" puisque les fautes sont barrées ; ou sinon "vu" voudrait dire "suffisamment faux pour que je ne m'embête pas à tout barrer" ?). Je comprends pas

Tu procède comme tu as dit dans le message précédent, et tu vas déduire tout seul que ton raisonnement est faux, essaye de déterminer Ker (f).

[chan79]

on pourrait simplement prendre
f(e1)=u=(2,1,0)
f(e2)=v=(5,-1,2)
f(e3)=-u-v=(-7,0,-2)
f(e4)=(0,0,0)

[Pierrot73]

Tu procède comme tu as dit dans le message précédent, et tu vas déduire tout seul que ton raisonnement est faux, essaye de déterminer Ker (f).

Merci de m'aider zaidoun ! Finalement, ce post me servira peut-être plus à moi qu'à Crazyfrog.

Voilà comment j'aurais fait, avec u (x, y, z, t) élément de R4.

"Stratégie" initiale :

La matrice d’une application linéaire se remplit par colonne. Chaque colonne correspond à la décomposition de l’image par f d’un élément de la base de l’espace de départ dans la base d’arrivée. Dans notre cas, la matrice de l’application linéaire f est une matrice à quatre colonnes et trois lignes.

Noyau de f :

Définition du noyau :

Donc

est une famille libre et génératrice. Donc . D'où, dim[Ker(f)] = 2.

Image de f :

D'après le théorème de la dimension, dim[Im(f)] = 4 - 2 = 2.
On choisit donc arbitrairement 2 vecteurs parmi les 4 vecteurs de la base canonique de R4. Je choisis de travailler avec e1 et e2 :
f(e1)=(2,1,0)
f(e2)=(5,-1,2)

Puis, vu qu'on passe de R4 dans R3, f(e4) = (0, 0, 0).

J'arrive donc à la matrice M suivante :
, avec a, b, et c des réels à définir par la suite

jusque là tout est bon, ou je suis déjà dans les choux ?

[aymanemaysae]

Pour ma part, j'ai trouvé que M =

Si ce résultat est juste, je peux le détailler, sinon je continuerai mes recherches.

[zaidoun]

Pour ma part, j'ai trouvé que M =

Si ce résultat est juste, je peux le détailler, sinon je continuerai mes recherches.

La matrice est déjà donnée par chan79. Pour votre matrice, j'ai vérifié le Ker est bon, pour l'image je n'ai pas vérifié mais je dirais c'est juste à condition que les deux premiers vecteurs colonnes (dans ta matrice) soient colinéaires aux vecteurs données au début, donc il suffit de vérifier cela!!!

[Pierrot73]

on pourrait simplement prendre
f(e1)=u=(2,1,0)
f(e2)=v=(5,-1,2)
f(e3)=-u-v=(-7,0,-2)
f(e4)=(0,0,0)

Bon, comme je vois que ma matrice se rapproche sensiblement de celle de chan79 (qui a juste la plupart du temps ), je vais finir mon raisonnement.

On a donc la matrice . Il reste à définir a, b, et c afin que

On a le système suivant :


Or, comme x=y=z, on simplifie par x (par exemple) et on trouve : a=-7, b=0, c=-2.

Je trouve donc la même matrice que chan79 (ouf !). Mais je ne comprends toujours pas pourquoi ma phrase "Tu sais qu'au moins 2 de ces vecteurs seront envoyés sur 0 puisque dim(Ker) = 2." est fausse. :mur:

Dans mon raisonnement, comme dim(Ker) = 2, on a bien 2 des 4 vecteurs de la base {ei} de R4 qui vont définir les vecteurs u pour lesquels f(u) = 0.

[zaidoun]

Je trouve donc la même matrice que chan79 (ouf !). Mais je ne comprends toujours pas pourquoi ma phrase "Tu sais qu'au moins 2 de ces vecteurs seront envoyés sur 0 puisque dim(Ker) = 2." est fausse. :mur: .

La réponse est dans ta matrice, t'as uniquement f(e_4)=0.

[Pierrot73]

La réponse est dans ta matrice, t'as uniquement f(e_4)=0.

D'accord !!! Je vois (enfin ...) pourquoi ce que j'ai écrit est faux. Merci !

Ce que je voulais dire initialement : "puisque dim(ker) = 2, on peut donc choisir 2 vecteurs au hasard parmi les 4 de {ei} bla bla ... puisque dim(ker) = 2, tu sais qu'un sev à deux dimensions est envoyé sur 0", ce qui est effectivement différent de ce que j'avais écrit

[aymanemaysae]

Soit ,

[Robot]

Des erreurs de signe, et tu n'as pas à répondre à la place de Crazyfrog

[chan79]

Si on choisit pour f(e1) et f(e2) deux combinaisons linéaires de u= (2,1,0) et v=(5,-1,2), par exemple f(e1)=u+v et f(e2)=u-v (f(e1) et f(e2) ne sont pas colinéaires)
il faut compléter la matrice



Quel que soit le réel k, l'image de (1,1,1,k) doit être (0,0,0)
donc ...

[Pierrot73]

Des erreurs de signe

Euh ... à qui réponds-tu Robot ? (dixit le gars toujours pas sûr de son résultat ...)

[Crazyfrog]

Si on choisit pour f(e1) et f(e2) deux combinaisons linéaires de u= (2,1,0) et v=(5,-1,2), par exemple f(e1)=u+v et f(e2)=u-v (f(e1) et f(e2) ne sont pas colinéaires)
il faut compléter la matrice



Quel que soit le réel k, l'image de (1,1,1,k) doit être (0,0,0)
donc ...

a=-4
b=-2
c=2
d=e=f=0