soit a,b,c,d, apartient Q et x apartien R/Q
Trouver une condition suffisante et nécessaire sur (a,b,c,d) pour que (ax+b)/(cx+d) eoit rationel?
Les Nombres Rationnels
8 messages
- Page 1 sur 1
Salut, si  alors
alors x=de-b\) et, si
et, si  était non nul, on aurait
était non nul, on aurait  ce qui est contraire à l'hypothèse.
ce qui est contraire à l'hypothèse.
Donc il faut que et donc
et donc x=0) et ces 2 conditions sont suffisante pour que
et ces 2 conditions sont suffisante pour que  .
.
- Soit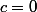 alors
alors  doit aussi être nul et quelque soient d et e (avec
doit aussi être nul et quelque soient d et e (avec 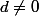 ) on a
) on a 
- Soit alors on doit avoir
alors on doit avoir  et il faut que
et il faut que  c'est à dire que
c'est à dire que 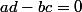 .
.
Donc il faut que
- Soit
- Soit
Modifié en dernier par Ben314 le 08 Avr 2018, 16:27, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut, sialors
et, si
était non nul, on aurait
ce qui est contraire à l'hypothèse.
Doncet donc
.
- Sialors
doit être nul et quelque soient d et e (avec
) on a
- Sialors on doit avoir
et il faut que
c'est à dire que
.
pas compris Si 4$c=0 alors a doit etre nul, et pour c defernt de 0?
Si
a) Si c = 0 et a
b) Si c = 0 , a = 0 et b = 0 , on a d = 0 : résultat aberrant.
c) Si c = 0 , a = 0 et b
Donc pour (a,b,c,d) = (0,b,0,d) avec b et d non nuls on a
d) Si d = 0 et b = 0 , on a r =
e) Si d = 0 et b
On a aussi pour (a,b,c,d) = (a,0,c,0) avec a
Conclusion :
Pour (a,b,c,d) = (0,b,0,d) avec b et d non nuls ou (a,b,c,d) = (a,0,c,0) avec a
aymanemaysae a écrit:est définie pour (c,d)
(0,0).
Si= r avec r
Q , on a:
a) Si c = 0 et a0 , on a x =

Q : résultat aberrant.
b) Si c = 0 , a = 0 et b = 0 , on a d = 0 : résultat aberrant.
c) Si c = 0 , a = 0 et b0 , on a r =
.
Donc pour (a,b,c,d) = (0,b,0,d) avec b et d non nuls on aest rationnel.
d) Si d = 0 et b = 0 , on a r =.
e) Si d = 0 et b0 , on a x =

Q : résultat aberrant.
On a aussi pour (a,b,c,d) = (a,0,c,0) avec aR et c
0 on a
est rationnel.
Conclusion :
Pour (a,b,c,d) = (0,b,0,d) avec b et d non nuls ou (a,b,c,d) = (a,0,c,0) avec aR et c
0 on a
est rationnel.
Où est-il condition suffisante et nécessaire ?
aymanemaysae a écrit:est un rationnel
(a,b,c,d) = (0,b,0,d) avec b et d non nuls ou (a,b,c,d) = (a,0,c,0) avec a
R et c
0.
Il vous reste à faire l'implication dans l'autre sens: qui est évidente.
Tout ceci, si ma démarche est exempte d'erreurs.
C'est effectivement faux, par exemple si (a,b,c,d)=(1,2,3,6) alors
La C.N.S. est donnée dans le premier post : c'est ad-bc=0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
