bonjour svp aide moi sur cette exercice
soit f une application croissante continue et positive de ]0,1]
dans R on pose Un=f(exp^-n) et Vn=1/n f(1/n)
queque soit n>=1
1-démontrer que la convergence de la série (;)Un) est équivalente a la convergence d'une integral impropre
-faire de méme pour (;) Vn )
2-en déduire que la série(;) Un) converge si seulement si si la série (;)Vn) converge
Exercice
2 messages
- Page 1 sur 1
par Ben314 » 14 Déc 2015, 23:09
Salut,
C'est LE truc a savoir faire les yeux fermés les comparaisons sommesintégrales.
Je te fait le début du premier :
Comme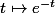
est décroissante de 
dans ]0,1] est que 
est croissante sur ]0,1], la fonction fonction composée )
est décroissante sur .
Donc, pour tout
et tout 
on a 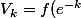\,\geq\, f(e^{-t})\,\geq\, f(e^{-(k+1)})=V_{k+1})
.
En intégrant de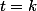
à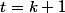 
on en déduit que \,dt\,\geq\, V_{k+1})
.
Puis, en sommant de k=1 à n (entier arbitraire) que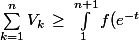\,dt\,\geq\, \sum_{k=2}^{n+1}V_{k})
.
Ce qui signifie que la série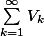
est de même nature que l'intégrale \,dt)
A toi la main...
C'est LE truc a savoir faire les yeux fermés les comparaisons sommesintégrales.
Je te fait le début du premier :
Comme
Donc, pour tout
En intégrant de
Puis, en sommant de k=1 à n (entier arbitraire) que
Ce qui signifie que la série
A toi la main...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :