Limite et continuité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ayalisa
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Nov 2015, 21:18
-
 par ayalisa » 10 Déc 2015, 00:31
par ayalisa » 10 Déc 2015, 00:31
Hi mes chers amis :ptdr: :ptdr:
Cet exo en analyse me parait vraimant tres sec
Est ce que on utilise une methode de proche en proche ?

Pour cette partie ( independante)
Comment construire le bon prolongement ?

Merci de m'indiquer le bon chemin , une petite indication :doh:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Déc 2015, 08:17
par Ben314 » 10 Déc 2015, 08:17
Salut,
Perso, pour le 1), je commencerais par montrer que, pour tout n dans N* et tout k de Z, on a
=f^n(x)+k)
, j'en déduirais que pour tout k de Z,
}{n}=\lim_{n\to\infty}\frac{f^n(0)}{n})
et je conclurais en utilisant la croissance de
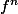
.
Pour le 2), sauf erreur, ça se fait très naturellement en utilisant les définitions (avec des epsilons) de la notion de limite et de la notion de continuité.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 10 Déc 2015, 15:24
par aymanemaysae » 10 Déc 2015, 15:24
On a la fonction g de IR dans IR telle que g(x)=f(x)-x.
Comme g est périodique de période 1, on a :
g(x+1)=g(x)+1 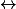 f(x+1)-(x+1)=f(x)-x
f(x+1)-(x+1)=f(x)-x 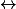 f(x+1)-1=f(x)
f(x+1)-1=f(x)
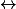 f(x+1)=f(x)+1
f(x+1)=f(x)+1 =f^1(x)+1) .
.
Supposons que pour k IN* on a
IN* on a =f^k(x)+1) et calculons
et calculons) .
.
 = f(f^k(x+1))=f(f^k(x)+1)=f(f^k(x))+1=f^{k+1}(x)+1,)
donc  k
k IN* on a
IN* on a =f^k(x)+1) .
.
Soit k IN*, supposons que pour h
IN*, supposons que pour h IN on a
IN on a =f^k(x)+h,) et calculons
et calculons ) .
.
=f^k(x+h)+1=f^k(x)+h+1,)
donc  h
h IN on a
IN on a =f^k(x)+h) .
.
De même on a :  h
h IN on a
IN on a =f^k((x-h)+h)=f^k(x-h)+h) ,
,
donc  =f^k(x)-h) ,
,
donc  h
h Z on a
Z on a =f^k(x)+h) .
.
Soit x=0, donc k
k IN* ,
IN* , h
h Z on a
Z on a=f^k(0)+h)
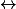
}{k}) =
=}{k}+\frac{h}{k}) ,
,
donc
}{k}) =
=
}{k}+\frac{h}{k}) =
=
}{k}) .
.
Soit x [-s,s] avec s
[-s,s] avec s IN*, et comme f est croissante, donc de même
IN*, et comme f est croissante, donc de même 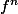 est croissante,
est croissante,
et on a 
}{k}) =
=
}{k})


}{k})


}{k}) =
=
}{k}) ,
,
donc 
}{k})


}{k}) ,
,
donc  x
x ]-
]- ,+
,+ [, on a
[, on a 
}{k})


}{k}) .
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités



