Conduction

[paaat]

bonjour a tous
j'ai un probleme en conduction

j'ai un cylindre de longueur L section S sur un axe x
-avec 2 temperatures differentes aux extremites
-traversé par une intensité I repartie uniformement


on me demande de faire un bilan d'energie pour trouver l'equa diff de la temperature mais je ne sai pas comment faire donc je fait un bilan de puissance mais j'ai un dx qui me gene :
je fait la puissance entre x et x+dx
ca me donne la derivé de jq multiplié par Sdx plus RI² =0

je dois mal m'y prendre
quelqu'un pourrait il m'expliquer

[flaja]

Bonjour paaat
Pour établir une équation différentielle,
on fait un bilan sur un volume élémentaire infiniment petit.
Il faut trouver une équation en fonction de "x".
On prend comme volume élémentaire S.dx de la position x à x+dx pendant le temps dt.
Bilan :
chaleur créé + chaleur entrante + chaleur sortante = gain de chaleur

* Il y a le dépôt d'énergie par effet Joule
Quel est la résistance R de "S.dx" ?
* Il y a le flux de chaleur entrant par conduction thermique ?
* Il y a le flux de chaleur sortant par conduction thermique ?
* Il y a la chaleur transportée par les électrons ??? à négliger car on ne sait pas le calculer
* Il y a les fuites thermiques sur les bords du cylindre ? à négliger car 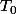ambiant n'est pas connu.
* Gain de chaleur : (élévation de température)

[paaat]

merci de ta reponse

j'ai oublié quelques precisions:
les parois sont adiabatiques
R c'est pour le cylindre entier
le systeme est en regime stationnaire
donc j'obtient

-lambda*d²T/dx²+RI²/L=0

est ce correcte car ca me parrait un peut leger pour une equa diff

[flaja]

Je suis d'accord avec ta formule,
à part que j'aurais un signe + devant lambda
car tient compte du fait que
ce qui permettra par ailleurs d'avoir une solution exponentielle décroissante au lieu d'une sinusoïde.